có câu này mấy bạn giúp nha
Cho đường tròn tâm o duong kinh AB Điểm M nằm trên đườn tròn (m ko =a=b)Tính góc
AMB
Những câu hỏi liên quan
Cho đường tròn tâm O đường kính AB. Gọi M là điểm nằm trên đường tròn, tính số đo góc AMB.
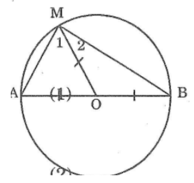
Nối OM, ta có:
OA = OM (bán kính đường tròn tâm O)
Nên ΔOAM cân tại O
⇒∠A =∠M1(tính chất tam giác cân)(1)
OM = OB (bán kính đường tròn tâm O)
Suy ra: ΔOBM cân tại O
⇒∠B =∠M2(tính chất tam giác cân) (2)
Trong ΔAMB ta có:
∠A + ∠AMB + ∠B = 180º (tổng ba góc trong tam giác)
⇒∠A +∠B +∠M1+∠M2 =180 (3)
Từ (1), (2) và (3) suy ra: 2(∠M1 + ∠M2)=180o
Vậy: ∠M1+∠M2=90o hay ∠(AMB) =90o
Đúng 0
Bình luận (0)
cho đường tròn tâm o đường kính ab. Gọi m là một điểm nằm trên đường tròn, tính số đo góc AMB
Cho đường tròn tâm O đường kính AB. Gọi M là một điểm nằm trên đường tròn, tính số đo góc AMB
cho đường tròn tâm o bán kính 3cm và một điểm m nằm ngoài đương tròn. qua m kẻ 2 tiếp tuyến ma,b với đường tròn ( a,b là tiếp điểm ) sao cho góc amb = 60 độ
a) tam giác amb là tam giác gì ?
b) qua điểm c trên cung nhỏ ab kẻ tiếp tuyến với đường tròn tâm o cắt ma và mb lần lượt tại n và q.tính góc NOQ
c, tính chứ vi tam giác MNQ
........................
.
Xem chi tiết
Giải thích các bước giải:
MO là t.p.g. của AMBˆAMB^
⇒AMOˆ=BMOˆ=AMBˆ2=450⇒AMO^=BMO^=AMB^2=450
⇒ΔAMO−và−ΔBMO⇒ΔAMO−và−ΔBMO vuông cân
=> OA = AM = MB = BO
=> OAMB là h.thoi có AMBˆ=900AMB^=900
=> OAMB là h.v.
b)
PMPQ=MP+MQ+PQPMPQ=MP+MQ+PQ
=(MP+PC)+(MQ+QC)=(MP+PC)+(MQ+QC)
=(MP+PA)+(MQ+QB)=(MP+PA)+(MQ+QB)
=MA+MB=MA+MB
=2OA=2OA
=2R=2R
c)
OP−là−t.p.g.−của−AOCˆOP−là−t.p.g.−của−AOC^
⇒COPˆ=12AOCˆ⇒COP^=12AOC^ (1)
OQ−là−t.p.g.−của−BOCˆOQ−là−t.p.g.−của−BOC^
⇒COQˆ=12BOCˆ⇒COQ^=12BOC^ (2)
Cộng theo vế của (1) và (2), ta có:
COPˆ+COQˆ=12(AOCˆ+BOCˆ)=12AOBˆCOP^+COQ^=12(AOC^+BOC^)=12AOB^
⇒POQˆ=450
Giải thích các bước giải:
MO là t.p.g. của AMBˆAMB^
⇒AMOˆ=BMOˆ=AMBˆ2=450⇒AMO^=BMO^=AMB^2=450
⇒ΔAMO−và−ΔBMO⇒ΔAMO−và−ΔBMO vuông cân
=> OA = AM = MB = BO
=> OAMB là h.thoi có AMBˆ=900AMB^=900
=> OAMB là h.v.
b)
PMPQ=MP+MQ+PQPMPQ=MP+MQ+PQ
=(MP+PC)+(MQ+QC)=(MP+PC)+(MQ+QC)
=(MP+PA)+(MQ+QB)=(MP+PA)+(MQ+QB)
=MA+MB=MA+MB
=2OA=2OA
=2R=2R
c)
OP−là−t.p.g.−của−AOCˆOP−là−t.p.g.−của−AOC^
⇒COPˆ=12AOCˆ⇒COP^=12AOC^ (1)
OQ−là−t.p.g.−của−BOCˆOQ−là−t.p.g.−của−BOC^
⇒COQˆ=12BOCˆ⇒COQ^=12BOC^ (2)
Cộng theo vế của (1) và (2), ta có:
COPˆ+COQˆ=12(AOCˆ+BOCˆ)=12AOBˆCOP^+COQ^=12(AOC^+BOC^)=12AOB^
⇒POQˆ=450vv
Câu 13. BRVT2009 Cho nửa đường tròn tâm O có đường kính AB 2R. Kẻ Ax, By vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng nửa mặt phẳng có bờ là đường thẳng AB). Qua điểm M thay đổi trên nửa đường tròn (M khác A, B), kẻ tiếp tuyến của nửa đường tròn lần lượt cắt Ax và By tại C và D. ① Chứng minh tứ giác ACMO nội tiếp được đường tròn. ② Chứng minh OC vuông góc với OD và 1/OC^2 +1/OD^2 1/R^2. ③ Xác định vị trí của M để (AC + BD) đạt giá trị nhỏ nhất.
Đọc tiếp
Câu 13. BRVT2009 Cho nửa đường tròn tâm O có đường kính AB = 2R. Kẻ Ax, By vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng nửa mặt phẳng có bờ là đường thẳng AB). Qua điểm M thay đổi trên nửa đường tròn (M khác A, B), kẻ tiếp tuyến của nửa đường tròn lần lượt cắt Ax và By tại C và D. ① Chứng minh tứ giác ACMO nội tiếp được đường tròn. ② Chứng minh OC vuông góc với OD và 1/OC^2 +1/OD^2 =1/R^2. ③ Xác định vị trí của M để (AC + BD) đạt giá trị nhỏ nhất.
1: Xét tứ giác OACM có
góc OAC+góc OMC=180 độ
=>OACM là tứ giác nội tiếp
2: Xét (O) có
CA,CM là tiếp tuyến
nên OC là đường phân giác của góc AOM(1)
Xét (O) có
DM,DB là tiếp tuyến
nen DM=DB và OD là phân giác của góc MOB(2)
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
=>OC vuông góc OD
=>1/OM^2=1/OC^2+1/OD^2=1/R^2
Đúng 0
Bình luận (0)
Cho đường tròn tâm O đường kính AB . M di động trên AB .N đối xứng với A qua M. P là giao điểm của BN và đường tròn tâm O . Q và R là giao điểm của đườn tròn tâm O . CHứng minh . a) N luôn nằm trên đường tròn đường kính ( C ) cố định tiếp xúc với đường tròn ( O ) .b ) RN là tiếp tuyến của đường tròn tâm C . c ) ARNQ là hình gì
Cho đường tròn tâm Ođường kính AB. Gọi M là một điểm nằm trên đường tròn, tính số đo góc AMB
vẽ hình làm chi tiết giúp mình
Bài : Cho đường tròn tâm O, đường kính AB, M là một điểm trên đường tròn, C là một điểm nằm giữa A và B. Qua M kẻ đường thẳng vuông góc với CM, đường thẳng này cắt các tiếp tuyến của đường tròn O kẻ từ A và B lần lượt tại E và F. Chứng minh rằng các tứ giác AEMC và BCMF nội tiếp
C là điểm nằm giữa A và B là sao bạn ? mình nghĩ AB là đường kính thì O là trung điểm AB rồi mà
Đúng 0
Bình luận (0)
cho đường tròn tâm (o) từ điểm M nằm ngoài đường tròn kẻ hai tiếp tuyến MA,MB với đườn tròn (o)(A và B là hai tiếp tuyến).Gọi I là giao điểm của OM và AB; từ B kẻ đườn kính BC của đường tròn(o),đường thẳng MC cắt đường tròn (o) tai D (D khác C)a)Chứng minh:4 điểm M,A,O,B cùng thuộc một đường trònb)Chứng minh:OM vuông với AB và MD.MCMI.MOc)Qua O vẽ đường thẳng vuông góc với MC tại E và cắt đường thẳng BA tại F. Chứng minh: FC là tiếp tuyến của đường tròn (O)
Đọc tiếp
cho đường tròn tâm (o) từ điểm M nằm ngoài đường tròn kẻ hai tiếp tuyến MA,MB với đườn tròn (o)(A và B là hai tiếp tuyến).Gọi I là giao điểm của OM và AB; từ B kẻ đườn kính BC của đường tròn(o),đường thẳng MC cắt đường tròn (o) tai D (D khác C)
a)Chứng minh:4 điểm M,A,O,B cùng thuộc một đường tròn
b)Chứng minh:OM vuông với AB và MD.MC=MI.MO
c)Qua O vẽ đường thẳng vuông góc với MC tại E và cắt đường thẳng BA tại F. Chứng minh: FC là tiếp tuyến của đường tròn (O)