Cho tam giác ABC vuông tại A . Biết AB=3cm,AC=4cm.Tìm AC

Những câu hỏi liên quan
cho tam giác vuông tại a,cạch ac=3cm,cạnh ab=4cm.tìm cạnh huyền bc.
Xét \(\Delta ABC\)vuông tại \(A\), ta có :
\(AB^2+AC^2=BC^2\) ( định lý \(Pi-ta-go\))
Mà \(AB=4\left(cm\right);AC=3\left(cm\right)\)
\(\Rightarrow4^2+3^2=BC^2\)
\(\Rightarrow16+9=BC^2\)
\(\Rightarrow BC^2=25\)
\(\Rightarrow BC=5\left(cm\right)\)
Vậy \(BC=5\left(cm\right)\)
~ Ủng hộ nhé
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Bài 1: Cho tam giác ABC vuông tại A, đường cao AH. a) Biết AB 9cm, BC 15cm. Tính BH, HC b) Biết BH 1cm, HC 3cm. Tính AB, AC c) Biết AB 6cm, AC 8cm. Tính AH, BCBài 2: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB 3cm, BH 2,4cm a) Tính BC, AC, AH, HC b) Tính tỉ số lượng giác của góc BBài 3: Cho tam giác ABC có BC 9cm, góc B 60 độ, góc C 40 độ, đường cao AH. Tính AH, AB, AC
Đọc tiếp
Bài 1: Cho tam giác ABC vuông tại A, đường cao AH.
a) Biết AB= 9cm, BC= 15cm. Tính BH, HC
b) Biết BH= 1cm, HC= 3cm. Tính AB, AC
c) Biết AB= 6cm, AC= 8cm. Tính AH, BC
Bài 2: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB= 3cm, BH= 2,4cm
a) Tính BC, AC, AH, HC b) Tính tỉ số lượng giác của góc B
Bài 3: Cho tam giác ABC có BC= 9cm, góc B= 60 độ, góc C= 40 độ, đường cao AH. Tính AH, AB, AC
Bài 1:
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH=\dfrac{9^2}{15}=\dfrac{81}{15}=5.4\left(cm\right)\)
Ta có: BH+CH=BC(H nằm giữa B và C)
nên CH=BC-BH=15-5,4=9,6(cm)
b) Ta có: BH+CH=BC(H nằm giữa B và C)
nên BC=1+3=4(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC=1\cdot4=4\left(cm\right)\\AC^2=CH\cdot BC=3\cdot4=12\left(cm\right)\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=2\left(cm\right)\\AC=2\sqrt{3}\left(cm\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
1) Cho tam giác ABC vuông tại A có góc B = 60độ, AC = 3cm. Tính BC, AB
2) Cho tam giác ABC vuông tại A có BC = 10cm, góc C = 3cm. Tính góc B, AB, AC
3) Cho tam giác ABC vuông tại A có AB = 4cm, góc B = 50 độ. Tính BC, góc C, AC
3:
góc C=90-50=40 độ
Xét ΔABC vuông tại A có sin C=AB/BC
=>4/BC=sin40
=>\(BC\simeq6,22\left(cm\right)\)
\(AC=\sqrt{BC^2-AB^2}\simeq4,76\left(cm\right)\)
1:
góc C=90-60=30 độ
Xét ΔABC vuông tại A có
sin B=AC/BC
=>3/BC=sin60
=>\(BC=\dfrac{3}{sin60}=2\sqrt{3}\left(cm\right)\)
=>\(AB=\dfrac{2\sqrt{3}}{2}=\sqrt{3}\left(cm\right)\)
Đúng 0
Bình luận (1)
Cho Tam giác ABC vuông tại A (AB < AC), đường cao AH. a) Chứng minh Tam giác HBA ~ tam giác ABC b) Chứng minh: AB^ = BH.BCTính AB, AH, biết BH = 3cm BC = 12cm c) Gọi E là trung điểm của AB, kẻ HD vuông góc với AC tại D (D thuộc AC). Đường thẳng CE cắt AH và HD lần lượt tại I, K. Chúng minh KH = KD và 3 điểm B, I, D thẳng hàng.
a: Xet ΔHBA và ΔABC có
góc BHA=góc BAC
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: ΔABC vuông tại A có AH vuông góc BC
nên BA^2=BH*BC
\(AB=\sqrt{3\cdot12}=6\left(cm\right)\)
\(AH=\sqrt{6^2-3^2}=3\sqrt{3}\left(cm\right)\)
c: Xet ΔCAE có KD//AE
nên KD/AE=CK/CE
Xét ΔCEB có KH//EB
nên KH/EB=CK/CE=KD/AE
mà AE=EB
nên KH=KD
Đúng 2
Bình luận (0)
câu 1:Cho tam giác ABC,vuông tại A,đường cáo AH(H thuộc BC).Biết AB12CM,Ac5cm.tính BH,CHCâu 2:cho tam giác ABC vuông tại A,đường cáo AH(H thuộc BC).Biết AB18cm,BH6cm.tính đô dài các cạnh AB,ACCâu 3:cho tam giac abc vuông tại a,biết ab-3cm,ac4cm,a.tinh bcb:kẻ đường cao ah,tính bhCâu 4:cho tam giác ABC Vuông tại A,biết ab4cm,đường cao ah2cm.Tính các góc và các cạnh còn lại của tam giác
Đọc tiếp
câu 1:Cho tam giác ABC,vuông tại A,đường cáo AH(H thuộc BC).Biết AB=12CM,Ac=5cm.tính BH,CH
Câu 2:cho tam giác ABC vuông tại A,đường cáo AH(H thuộc BC).Biết AB=18cm,BH=6cm.tính đô dài các cạnh AB,AC
Câu 3:cho tam giac abc vuông tại a,biết ab-3cm,ac=4cm,
a.tinh bc
b:kẻ đường cao ah,tính bh
Câu 4:cho tam giác ABC Vuông tại A,biết ab=4cm,đường cao ah=2cm.Tính các góc và các cạnh còn lại của tam giác
Câu 1:
Áp dụng đ/lí pytago vào tam giác ABC vuông tại A CÓ:AB^2+AB^2=BC^2
Hay: 12^2+5^2=169=BC^2
=> BC=13cm
ÁP dụng hệ thức ta có:
+) AB^2=BH.BC
Hay: BH=AB^2:BC=144:13 =144/13(cm)
Ta có CH=BC-BH=13-144/13=25/13(cm)
Đúng 0
Bình luận (0)
Bạn chỉ cần áp dụng hệ thức lượng là đc rồi o0o
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A , đường cao AH . Chứng minh rằng 1/AH^2=1/AB^2+1/ac^2
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A biết AB =3cm AC=4cm tính AH HB

xét tam giác ABC vuông tại A đường cao AH , áp dụng đinh lí Pytago ta có
\(AB^2+AC^2=BC^2< =>BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5cm\)
ta có: \(AH.BC=AB.AC\)(hệ thức lượng tam giác vuông)
=>
\(AH=\dfrac{AB.AC}{BC}=\dfrac{3.4}{5}=\dfrac{12}{5}=2,4cm\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A. Đường tròn (O) nội tiếp tam giác ABC tiếp xúc với AB, AC lần lượt tại D và E. Tính bán kính của đường tròn (O) biết AB = 3cm, AC = 4cm.
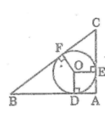
Áp dụng định lí Pitago vào tam giác vuông ABC ta có :
B C 2 = A B 2 + A C 2 = 3 2 + 4 2 = 25
Suy ra : BC = 5 (cm)
Theo tính chất hai tiếp tuyến giao nhau ta có:
AD = AE
BD = BF
CE = CF
Mà: AD = AB – BD
AE = AC – CF
Suy ra: AD + AE = AB – BD + (AC – CF)
= AB + AC – (BD + CF)
= AB + AC – (BF + CF)
= AB + AC – BC
Suy ra:
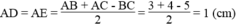
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, kẻ tia phân giác góc ABC cắt AC tại D. Biết BC = 5cm, AB = 3cm
a) Tính AC và AD
b) Kẻ DE // AB (E thuộc BC). Tính DE
a, Theo định lí Pytago tam giác ABC vuông tại A
\(AC=\sqrt{BC^2-AB^2}=4cm\)
Vì BD là pg nên \(\dfrac{AB}{BC}=\dfrac{AD}{DC}\Rightarrow\dfrac{DC}{BC}=\dfrac{AD}{AB}\)
Theo tc dãy tỉ số bằng nhau
\(\dfrac{DC}{BC}=\dfrac{AD}{AB}=\dfrac{4}{8}=\dfrac{1}{2}\Rightarrow DC=\dfrac{5}{2}cm;AD=\dfrac{3}{2}\)cm
b, Vì DE // AB Theo hệ quả Ta lét
\(\dfrac{DC}{AC}=\dfrac{DE}{AB}\Rightarrow DE=\dfrac{AB.DC}{AC}=\dfrac{15}{8}\)cm
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Vẽ HM ⊥ AB;HN ⊥ AC. Biết AB = 3cm; AC = 4 cm
b) Tính số đo các góc của tam giác AMN
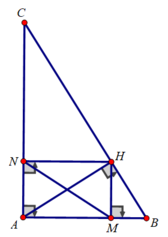
b) Xét tam giác AHB vuông tại H, HM là đường cao có:

∠(AMN) + ∠(ANM ) = 90 0 ⇒ ∠(ANM ) = 90 0 - ∠(AMN) = 53 , 1 0
Đúng 0
Bình luận (0)























