Cho hình chóp tứ giác S.ABCD có đáy là hình chữ nhật có các cạnh A B = a , A D = a 2 , S A ⊥ A B C D , góc giữa SC và đáy bằng 60 ° . Thể tích hình chóp S.ABCD bằng
A. 2 a 3
B. 3 2 a 3
C. a 3
D. 6 a 3
Cho hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AB = a, AD = a 2 , SA⊥(ABCD) góc giữa SC và đáy bằng 60°. Thể tích hình chóp S.ABCD bằng:
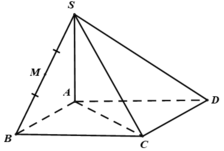
A. a 3 2
B. 3 a 3 2
C. 3 a 3
D. a 3 6
Đáp án A
Theo bài ra ta có:
SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
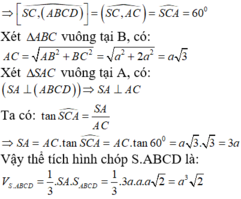
Hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AB = a, AD = a 2 ; SA ⊥ (ABCD), góc giữa SC và đáy bằng 60°. Thể tích hình chóp S.ABCD bằng:
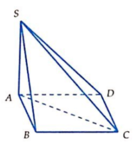
A. a 3 2
B. 3 a 3
C. a 3 6
D. 3 a 3 2
Hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AB = a, AD = a 2 , SA⊥(ABCD) góc giữa SC và đáy bằng 60°. Thể tích hình chóp S.ABCD bằng:
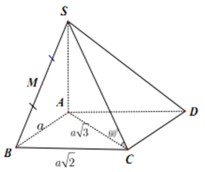
A. a 3 2
B. a 3 6
C. 3 a 3
D. 3 a 3 2
Đáp án A
SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
Xét ΔABC vuông tại B, có

Cho hình chóp tứ giác S.ABCD có đáy là hình chữ nhật có các cạnh ![]() , góc giữa SC và đáy bằng
60
o
. Thể tích hình chóp S.ABCD bằng
, góc giữa SC và đáy bằng
60
o
. Thể tích hình chóp S.ABCD bằng
![]()
![]()
![]()
![]()
Hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh A B = a , A D = a 2 , S A ⊥ ( A B C D ) góc giữa SC và đáy bằng 60°. Thể tích hình chóp S.ABCD bằng:
A. 2 a 3
B. 6 a 3
C. 3 a 3
D. 3 2 a 3
Chọn A.
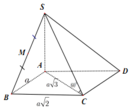
SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD)

Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình chữ nhật, cạnh A B = a , A D = 2 a , cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa cạnh SD và mặt phẳng đáy bằng 60 o . Thể tích V của khối chóp S.ABCD là
A. V = 2 a 3 3 .
B. V = 4 a 3 3 .
C. V = a 3 3 .
D. V = 4 a 3 3 .
Cho hình chóp tứ giác S . A B C D có đáy ABCD là hình chữ nhật có cạnh bên SA vuông góc với mặt phẳng đáy và S A = a 2 . Thể tích V của khối chóp S.ABCD là :
A. V = 2 2 9 a 3
B. V = 2 3 a 3
C. 2 2 a 3
D. V = 2 2 3 a 3
Đáp án D
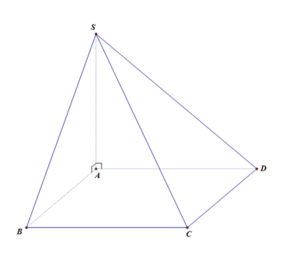
V S . A B C D = 1 3 S A B C D . S A = 1 3 . A B . A D . S A = 1 3 a . 2 a . a 2 = 2 2 a 3 3 .
Cho chóp tứ giác \(S.ABCD\) có đáy là hình chữ nhật với \(AB = 4a,\) \(AD = 3a\). Các cạnh bên đều có độ dài \(5a\). Góc nhị diện \(\left[ {S,BC,A} \right]\) có số đo là
A. \({75^ \circ }46'\).
B. \({71^ \circ }21'\).
C. \({68^ \circ }31'\).
D. \({65^ \circ }12'\).
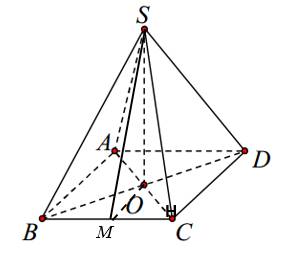
Gọi \(M\) là trung điểm \(BC\).
Ta có:\(OM=\dfrac{1}{2}.AB=2a;AC=\sqrt{AB^2+BC^2}=5a;OC=\dfrac{1}{2}AC=\dfrac{5}{2}a\)
\(SO=\sqrt{SC^2-OC^2}=\dfrac{5\sqrt{3}}{2}a\)
\(\left[S,BC,A\right]=\widehat{SMO}\)
\(\tan\widehat{SMO}=\dfrac{SO}{OM}=\dfrac{5\sqrt{3}}{4}\)
Suy ra:\(\widehat{SMO}=65,2^o\)
\(\Rightarrow D\)
Cho hình chóp tứ giác S.ABCD có đáy là hình chữ nhật, AB = a, AD = a 2 . Biết SA ⊥ ABCD và góc giữa đường thẳng SC với mặt phẳng đáy bằng 45 0 . Thể tích khối chóp S. ABCD bằng:
A . a 3 2
B . 3 a 3
C . a 3 6
D . a 3 6 3
Đáp án D
Dễ thấy ![]()
Lại có ∆SAC vuông tại A
=> AC = SA = ![]()
Vậy VS.ABCD = ![]()