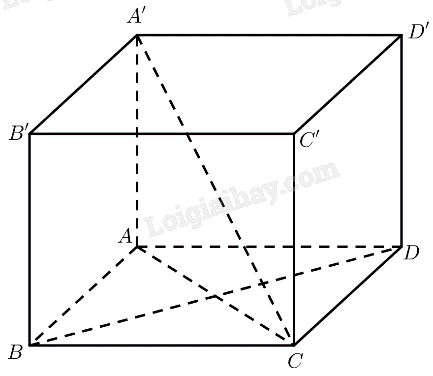
Tính thể tích khối lập phương ABCD.A'B'C'D' biết độ dài đoạn thẳng AC=2a.
A. 2 a 3 2 3 .
B. 2 a 3 2 .
C. a 3
D. a 3 3 .
Tính thể tích khối lập phương ABCD.A'B'C'D' biết độ dài đoạn thẳng AC = 2a.
A . 2 a 3 2 3
B . 2 a 3 2
C . a 3
D . a 3 3
Đáp án B
Ta có AC = 2a => cạnh của hình lập phương là
2
a![]()
Cho hình lăng trụ đứng \(ABCD.A'B'C'D'\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(B\), \(AA' = 2a,AD = 2a,AB = BC = a\).
a) Tính độ dài đoạn thẳng \(AC'\).
b) Tính tổng diện tích các mặt của hình lăng trụ.
a) \(\Delta ABC\) vuông cân tại \(B \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \)
\(CC' = AA' = 2a\)
\(CC' \bot \left( {ABCD} \right) \Rightarrow CC' \bot AC\)
\( \Rightarrow \Delta ACC'\) vuông tại \(C \Rightarrow AC' = \sqrt {A{C^2} + CC{'^2}} = a\sqrt 6 \)
b) \({S_{ABC{\rm{D}}}} = {S_{A'B'C'C'}} = \frac{1}{2}\left( {A{\rm{D}} + BC} \right).AB = \frac{{3{a^2}}}{2}\)
Gọi \(M\) là trung điểm của \(AD\)
\( \Rightarrow ABCM\) là hình vuông\( \Rightarrow MC = M{\rm{D}} = MA = \frac{1}{2}A{\rm{D}} = a\)
\(\Delta MC{\rm{D}}\) vuông cân tại \(M \Rightarrow C{\rm{D}} = \sqrt {C{M^2} + D{M^2}} = a\sqrt 2 \)
\(\begin{array}{l}{S_{ABB'A'}} = AB.AA' = 2{a^2}\\{S_{ADD'A'}} = AD.AA' = 4{a^2}\\{S_{BCC'B'}} = BC.CC' = 2{a^2}\\{S_{C{\rm{DD}}'{\rm{C}}'}} = C{\rm{D}}.CC' = 2{a^2}\sqrt 2 \end{array}\)
Tổng diện tích các mặt của hình lăng trụ là:
\(\begin{array}{l}S = {S_{ABC{\rm{D}}}} + {S_{A'B'C'C'}} + {S_{ABB'A'}} + {S_{ADD'A'}} + {S_{BCC'B'}} + {S_{C{\rm{DD}}'{\rm{C}}'}}\\ & = \frac{{3{a^2}}}{2} + \frac{{3{a^2}}}{2} + 2{a^2} + 4{a^2} + 2{a^2} + 2{a^2}\sqrt 2 = \left( {11 + 2\sqrt 2 } \right){a^2}\end{array}\)
Cho hình lập phương ABCD.A'B'C'D' có AC = 5cm. Hãy tính:
a) Độ dài cạnh hình lập phương;
b) Độ dài đường chéo hình lập phương;
c) Thể tích hình lập phương.
Cho hình hộp đứng \(ABCD.A'B'C'D'\) có đáy là hình thoi. Cho biết \(AB = BD = a,A'C = 2a\).
a) Tính độ dài đoạn thẳng \(AA'\).
b) Tính tổng diện tích các mặt của hình hộp.
a) Xét tam giác \(AB{\rm{D}}\) có: \(AB = A{\rm{D}} = B{\rm{D}} = a\)
\( \Rightarrow \Delta AB{\rm{D}}\) đều \( \Rightarrow \widehat {BA{\rm{D}}} = {60^ \circ } \Rightarrow \widehat {ABC} = {180^ \circ } - \widehat {BA{\rm{D}}} = {120^ \circ }\)
Xét tam giác \(AB{\rm{C}}\) có:
\(AC = \sqrt {A{B^2} + B{C^2} - 2.AB.BC} = a\sqrt 3 \)
\(AA' \bot \left( {ABCD} \right) \Rightarrow AA' \bot AC \Rightarrow \Delta AA'C\) vuông tại \(A\)
\( \Rightarrow AA' = \sqrt {A'{C^2} - A{C^2}} = a\)
b) Ta có:
\(\begin{array}{l}{S_{ABC{\rm{D}}}} = {S_{A'B'C'D'}} = AB.AC.\sin \widehat {BAC} = \frac{{{a^2}\sqrt 3 }}{2}\\{S_{ABB'A'}} = {S_{C{\rm{DD}}'{\rm{C}}'}} = AB.AA' = {a^2}\\{S_{A{\rm{DD}}'A'}} = {S_{BCC'B'}} = A{\rm{D}}.AA' = {a^2}\end{array}\)
Tổng diện tích các mặt của hình hộp là:
\(S = {S_{ABC{\rm{D}}}} + {S_{A'B'C'D'}} + {S_{ABB'A'}} + {S_{C{\rm{DD}}'{\rm{C}}'}} + {S_{A{\rm{DD}}'A'}} + {S_{BCC'B'}} = 2.\frac{{{a^2}\sqrt 3 }}{2} + 4.{a^2} = \left( {4 + \sqrt 3 } \right){a^2}\)
Trên đường thẳng x,y lấy 3 điểm A,B,C biết độ dài đoạn thẳng AB=a,độ dài đoạn thẳng AC=2a (a>0).Tính độ dài đoạn thẳng BC theo a
Tính thể tích V của khối lập phương ABCD.A'B'C'D' biết đường chéo AC'=a 3 .
A. a 3 3
B. 3 3 a 3
C. 3 6 a 3 4
D. a 3
Chọn D.
Gọi cạnh hình lập phương là x. Ta có
![]()
Cho hình lập phương ABCD.A'B'C'D'.
a) Chứng minh đường thẳng BC' vuông góc với mặt phẳng (A'B'CD)
b) Xác định và tính độ dài đoạn vuông góc chung của AB' và BC'.
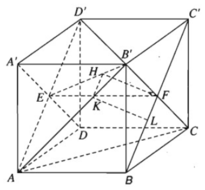
a) Ta có B'C ⊥ BC' vì đây là hai đường chéo của hình vuông BB'C'C
Ngoài ra ta còn có: A'B' ⊥ (BB'C'C) ⇒ A'B' ⊥ BC'
Từ đó ta suy ra BC' ⊥ (A'B'CD) vì mặt phẳng (A'B'CD) chứa đường thẳng A'B' và B'C cùng vuông góc với BC'.
b) Mặt phẳng (AB'D') chứa đường thẳng AB' và song song với BC', ta hãy tìm hình chiếu của BC' trên mặt phẳng (AB'D'). Gọi E, F lần lượt là tâm các hình vuông ADD'A', BCC'B'. Kẻ FH ⊥ EB'với H ∈ EB', khi đó FH nằm trên mặt phẳng (A'B'CD) nên theo câu a) thì FH ⊥ (AB'D'), do đó hình chiếu BC' trên mặt phẳng (AB'D) là đường thẳng đi qua H và song song với BC'. Giả sử đường thẳng đó cắt AB' tại K thì từ K vẽ đường thẳng song song với FH cắt BC' tại L. Khi đó KL là đoạn vuông góc chung cần dựng. Tam giác B'EF vuông tại F nên từ công thức
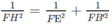
ta tính được
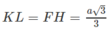
Nhận xét . Độ dài đoạn vuông góc chung của AB' và BC' bằng khoảng cách giữa hai mặt phẳng song song (AB'D') và (BC'D) lần lượt chứa hai đường thẳng đó.
Khoảng cách này bằng 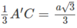
Tính thể tích của khối lập phương ABCD.A'B'C'D' biết AD' = 2a
A. V = a 3
B. V = 8 a 3
C. V = 2 2 a 3
D. V = 2 2 3 a 3
Đáp án C
Ta có ![]()
![]()
Vậy cạnh của hình lập phương trình có cạnh độ dài 2 a.
Vậy ![]()
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Điểm M thuộc đoạn thẳng BC' , điểm N thuộc đoạn thẳng AB' tạo với mặt phẳng đáy một góc 30 0 . Tìm độ dài nhỏ nhất của đoạn thẳng MN.
A . a 2
B . 2 a 3
C . 2 a 5 - 1
D . 2 a 5 + 1
Đáp án D
Ý tưởng: 1 - MN phải chăng sẽ là hai điểm đặc biệt nào đó
2 – Khi nhận ra M là trung điểm của BA’ thì ta tiến hành tính toán MN qua điểm A’ bằng cách lấy P thuộc BC’!

Lời giải: Dễ có mặt phẳng (BA’C’) vuông góc với AB’. Do đó để MN là nhỏ nhất thì M là giao của AB’ và BA’, N là điểm thuộc BC’ sao cho góc giữa MN và (A’B’C’D’) là 30 0 . Gọi P là điểm thuộc BC’sao cho A’P cũng hợp với mặt phẳng đáy một góc 30 0 , khi đó MN là đường trung bình của tam giác BA’P nên MN = 1 2 A'P.
Giả sử độ dài đoạn B’H = x, khi đó PH = HC’ = a – x (tam giác PC’H vuông cân tại C’), và A'H = ![]()
Theo điều ta đã giả sử ở trên thì góc giữa A’P và (A’B’C’D’) = 30 0 , do đó
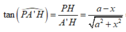
![]()
Mặt khác ta lại có A'P = ![]()
![]() (2)
(2)
Từ (1) và (2) ta tính được ![]()
Từ đây ta rút ra được![]()
=> Chọn phương án D.