Các giá trị thực của tham số m để phương trình 12 x + ( 4 - m ) 3 x - m = 0 có nghiệm thuộc khoảng (-1;0) là:
A. m ∈ 17 16 ; 5 2
B. m ∈ 2 ; 4
C. m ∈ 5 2 ; 6
D. m ∈ 1 ; 5 2
Tìm tất cả các giá trị thực của tham số m để bất phương trình m 5 − x + 4 − x = x x + x + 12 có nghiệm.
A. 2 15 − 4 3 ≤ m ≤ 12
B. 2 15 − 4 3 < m < 12
C. m ≤ 12
D. m ≥ 2 15 − 4 3
Đáp án A
Tập xác định của hàm số: D = 0 ; 4
Ø Xét tử số, đặt g x = x x + x + 12
Em thấy g x > 0 ∀ x ∈ 0 ; 4 g ' x = 3 x 2 x + 1 2 x + 12 > 0 ⇒ g x là hàm dương và đồng biến trên [0;4]
Ø Xét mẫu số, xét h x = 5 − x + 4 − x
Em thấy h x > 0 ∀ x ∈ 0 ; 4 h ' x = − 1 2 5 − x + − 1 2 4 − x < 0
=> h(x) là hàm dương và nghịch biến trên [0;4]
=> 1 h x là hàm đồng biến trên [0;4] ⇒ y = g x . 1 h x là hàm đồng biến trên [0;4]
⇒ maxy = y 4 = 12 ; miny = y 0 = 2 15 − 4 3
Tìm tất cả các giá trị thực của tham số m để phương trình sau có nghiệm x ∈ [ 1 ; 2 ] .
x 4 + 16 x 4 + 4 ( x 2 + 4 x 2 ) - 12 ( x - 2 x ) = m
A. - 13 ≤ m ≤ 11
B. - 15 ≤ m ≤ 9
C. - 15 < m < 9
D. - 16 ≤ m ≤ 9
Đáp án là B.
Đặt t = x - 2 x Đạo hàm t , = 1 + 2 x 2 > 0
Do đó t ( 1 ) ≤ t ≤ t ( 2 ) , ∀ x ∈ [ 1 ; 2 ] , suy ra - 1 ≤ t ≤ 1
Ta có x 2 + 4 x 2 = t 2 + 4 , x 4 + 16 x 4 = ( x 2 + 4 x 2 ) 2 - 8 = ( t 2 + 4 ) 2 - 8 = t 4 + 8 t 2 + 8
Phương trình đã cho trở thành
t 4 + 8 t 2 + 8 - 4 ( t 2 + 4 ) - 12 t = m ⇔ t 4 + 4 t 2 - 12 t = m + 8 ( * )
Phương trình đã cho có nghiệm trong đoạn [1;2] khi và chỉ khi phương trình (*) có nghiệm trong [-1;1] Xét hàm số y=f(t)= t 4 + 4 t 2 - 12 t trên [-1;1]
Đạo hàm y , = 4 t 8 + 8 t - 12 , t ∈ ( - 1 ; 1 ) . y , = 4 ( t - 1 ) ( t 2 + t + 3 ) < 0 , ∀ t ∈ ( - 1 ; 1 )
Bảng biến thiên:
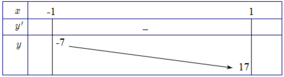
Do đó để phương trình đã cho có nghiệm trên [1;2] thì - 7 ≤ m + 8 ≤ 17 ⇔ - 15 ≤ m ≤ 9
tìm tất cả các giá trị thực của tham số m để phương trình x-4√(x+3 ) + m = 0 có 2 nghiệm phân biệt
\(x-4\sqrt{x+3}+m=0\)
\(\Leftrightarrow x+3-4\sqrt{x+3}-3+m=0\left(1\right)\)
\(đăt:\sqrt{x+3}=t\left(t\ge0\right)\)
\(\left(1\right)\Leftrightarrow t^2-4t-3+m=0\Leftrightarrow f\left(t\right)=t^2-4t-3=-m\left(2\right)\)
\(\left(1\right)-có-2ngo-phân-biệt\Leftrightarrow\left(2\right)có-2ngo-phân-biệt-thỏa:t\ge0\)
\(\Rightarrow f\left(0\right)=-3\)
\(\Rightarrow f\left(t\right)min=\dfrac{-\Delta}{4a}=-7\Leftrightarrow t=2\)
\(\Rightarrow-7< -m\le-3\Leftrightarrow3\le m< 7\)
Cho bất phương trình 3 + x + 1 - x ≤ m + 1 - x 2 - 2 x . Tìm tất cả các giá trị thực của tham số m để bất phương trình có nghiệm thực.
A. m ≥ 25 4
B. m ≥ 4
C. m ≥ 6
D. m ≥ 7
Cho phương trình ( x + x + 1 ) ( m x + 1 + 1 x + 16 x 2 + x 4 ) = 1 với m là tham số thực. Tìm số các giá trị nguyên của m để phương trình có hai nghiệm thực phân biệt
A. 3.
B. 4.
C. 5.
D. 6
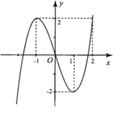
Hình bên là đồ thị của hàm số y = x 3 - 3 x Tìm tất cả các giá trị thực của tham số m để phương trình 64 | x | 3 = ( x 2 + 1 ) 2 ( 12 | x | + m ( x 2 + 1 ) ) có nghiệm.
A.![]()
B. Với mọi m
C. ![]()
D. ![]()
Đáp án A
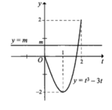
![]() (*)
(*)
Đặt ![]()
Yêu cầu bài toán trở thành: Tìm m để phương trình ![]() có nghiệm
có nghiệm ![]()
Từ đồ thị đã cho, ta suy ra đồ thị của hàm số ![]()
Từ đó ta có kể quả thỏa mãn yêu cầu bài toán ![]()
Cho phương trình log 2 x = m với x > 0. Tìm tất cả các giá trị thực của tham số m để phương trình có nghiệm thực.
A. m ≥ 0
B. m ∈ ℝ
C. m > 0
D. m ∈ ℤ
Đáp án là B
Tập giá trị của hàm số log a x = R
Câu 1 a.tìm tất cả các giá trị của tham số m để bất phương trình mx²+3mx+(m+1)>0 nghiệm đúng với mọi số thực x? b.tìm các giá trị của m để biểu thức sau luôn âm:g(x)=(m-4)x²+(2m-8)x+m-5
a: Trường hợp 1: m=0
Bất phương trình sẽ là \(0x^2+3\cdot0\cdot x+0+1>0\)
=>1>0(luôn đúng)
Trường hợp 2: m<>0
\(\text{Δ}=\left(3m\right)^2-4m\left(m+1\right)\)
\(=9m^2-4m^2-4m=5m^2-4m\)
Để phương trình có nghiệm đúng với mọi số thực x thì \(\left\{{}\begin{matrix}m\left(5m-4\right)< 0\\m>0\end{matrix}\right.\Leftrightarrow0< m< \dfrac{4}{5}\)
Vậy: 0<=m<4/5
b: Trường hợp 1: m=4
\(g\left(x\right)=\left(4-4\right)\cdot x^2+\left(2\cdot4-8\right)x+4-5=-1< 0\)(luôn đúng)
Trường hợp 2: m<>4
\(\text{Δ}=\left(2m-8\right)^2-4\left(m-4\right)\left(m-5\right)\)
\(=4m^2-32m+64-4\left(m^2-9m+20\right)\)
\(=4m^2-32m+64-4m^2+36m-80\)
=4m-16
Để bất phương trình luôn âm thì \(\left\{{}\begin{matrix}4m-16< 0\\m-4< 0\end{matrix}\right.\Leftrightarrow m< 4\)
Vậy: m<=4
Câu 1 a.tìm tất cả các giá trị của tham số m để bất phương trình mx²+3mx+(m+1)>0 nghiệm đúng với mọi số thực x?
b.tìm các giá trị của m để biểu thức sau luôn âm:g(x)=(m-4)x²+(2m-8)x+m-5
Cho phương trình m + 2 2 + x - 2 2 - x + 3 x + 4 4 - x 2 = m + 12 . Số giá trị nguyên của tham số m để phương trình đã cho có hai nghiệm thực phân biệt là
A. 3
B. 4
C. 2.
D. 5