Nếu hai đường thẳng xx’ , yy’ cắt nhau tại O và góc xOy vuông thì các góc x’Oy’ ; yOx’ ; xOy’ đều là góc vuông.”
a. Hãy vẽ hình theo định lý
b. Viết giả thiết và kết luận của định lý .
Những câu hỏi liên quan
a/ Hai đường thẳng xx’, yy’ cắt nhau tại điểm O và góc xOy bằng 900 . Hãy đo và cho biết số đo của các góc yOx’, x’Oy’, y’Ox
b/ Hai đường thẳng xx’, yy’ cắt nhau tại điểm O và góc xOy bằng 300 . Hãy đo và cho biết số đo của các góc yOx’, x’Oy’, y’Ox
a ) Ta có : xOy + yOx ' = 180 ( kề bù )
\(\Rightarrow\) 90 + yOx ' = 180
\(\Rightarrow\) yOx ' = 180 - 90 = 90
Lại có : xOy + y ' Ox = 180 ( kề bù )
\(\Rightarrow\) 90 + y ' Ox = 180
\(\Rightarrow\) y ' Ox = 180 - 90 = 90
Ta thấy : xOy ' + y ' Ox ' = 180 ( kề bù )
\(\Rightarrow\) 90 + y ' Ox ' = 180
\(\Rightarrow\) y ' Ox ' = 180 - 90 = 90
b ) Ta có : xOy + yOx ' = 180 ( kề bù )
\(\Rightarrow\) 30 + yOx ' = 180
\(\Rightarrow\) yOx ' = 180 - 30 = 150
Lại có : xOy + yOx '= 180 ( kề bù )
\(\Rightarrow\) 30 + yOx ' = 180
\(\Rightarrow\) yOx ' = 180 - 30 = 150
Ta thấy : x ' Oy + y ' Ox ' = 180 ( kề bù )
\(\Rightarrow\) 150 + y ' Ox ' = 180
⇒ y ' Ox ' = 180 - 150 = 3
Bài làm lại :
a ) \(\widehat{xOy}+\widehat{y'Oy}=180^o\)( KB )
\(\widehat{x'Oy}=180^o-\widehat{xOy}=180^o-90^o=90^o\)( Đối đỉnh )
Vậy \(\widehat{xOy}'=\widehat{y'Ox}=90^o\)( Đối đỉnh )
b ) \(\widehat{xOy}+\widehat{x'Oy}=180^o\)( KB )
\(\widehat{x'Oy}=180^o-\widehat{xOy}=180^o-30^o=150^o\)
Vậy \(\widehat{xOy}=\widehat{x'Oy'}=30^o\)( Đối đỉnh )
\(\widehat{yOx'}=\widehat{y'Ox}=150^o\)( Đối đỉnh )
Hai đường thẳng xx’ và yy’ cắt nhau tại O sao cho góc xOy vuông (H.3.8). Khi đó các góc yOx’, x’Oy’, xOy’ cũng đều là góc vuông. Vì sao?
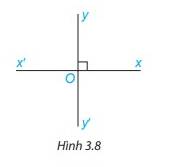
Góc x’Oy’ và xOy là hai góc đối đỉnh nên \(\widehat {x'Oy'} = \widehat {xOy} = 90^\circ \)
Góc xOy’ và xOy là hai góc kề bù nên
\(\begin{array}{l}\widehat {xOy'} + \widehat {xOy} = 180^\circ \\ \Rightarrow \widehat {xOy'} + 90^\circ = 180^\circ \\ \Rightarrow \widehat {xOy'} = 180^\circ - 90^\circ = 90^\circ \end{array}\)
Góc x’Oy và xOy là hai góc kề bù nên
\(\begin{array}{l}\widehat {x'Oy} + \widehat {xOy} = 180^\circ \\ \Rightarrow \widehat {x'Oy} + 90^\circ = 180^\circ \\ \Rightarrow \widehat {x'Oy} = 180^\circ - 90^\circ = 90^\circ \end{array}\)
Đúng 1
Bình luận (0)
a/ Hai đường thẳng xx’, yy’ cắt nhau tại điểm O và góc xOy bằng 90 độ . Hãy đo và cho biết số đo của các góc yOx’, x’Oy’, y’Ox
b/ Hai đường thẳng xx’, yy’ cắt nhau tại điểm O và góc xOy bằng 30 độ . Hãy đo và cho biết số đo của các góc yOx’, x’Oy’, y’Ox
a/ Hai đường thẳng xx’, yy’ cắt nhau tại điểm O và góc xOy bằng 900.
Hãy đo và cho biết số đo của các góc yOx’, x’Oy’, y’Ox
b/ Hai đường thẳng xx’, yy’ cắt nhau tại điểm O và góc xOy bằng 300.
Hãy đo và cho biết số đo của các góc yOx’, x’Oy’, y’Ox
Bài giải
a) yOx' ; x'Oy' ; y'Ox đều bằng 90 độ
b) yOx' bằng 150 độ ; x'Oy' bằng 30 độ ; y'Ox bằng 150 độ
Học tốt !
Cho hai đường thẳng xx’ và yy’ cắt nhau tại O. Góc xOy = 900. Chứng minh góc x’Oy, xOy’ và x’Oy’ vuông
mọi người làm nhanh giúp mk với ạ , mk đang vội
Ta có: \(\widehat{xOy}=90^0\)
nên \(xx'\perp yy'\)
\(\Leftrightarrow\left\{{}\begin{matrix}\widehat{xOy'}=90^0\\\widehat{x'Oy'}=90^0\\\widehat{x'Oy}=90^0\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Cho hai đường thẳng xx’ và yy’ cắt nhau tại O (H.3.5)
a) Dự đoán xem hai góc xOy và x’Oy’ có bằng nhau không?
b) Đo rồi so sánh số đo hai góc xOy và x’Oy’
a) Em dự đoán xem hai góc xOy và x’Oy’ có bằng nhau.
b) \(\widehat{xOy} = \widehat{x’Oy’} = 31^0\)
Đúng 0
Bình luận (0)
Chứng minh định lí: “Nếu hai đường thẳng xx’, yy’ cắt nhau tại O và góc xOy vuông thì các góc đều là góc vuông”.
Đọc tiếp
Chứng minh định lí: “Nếu hai đường thẳng xx’, yy’ cắt nhau tại O và góc xOy vuông thì các góc đều là góc vuông”.
Chứng minh định lí: “Nếu hai đường thẳng xx’, yy’ cắt nhau tại O và góc xOy vuông thì các góc đều là góc vuông”.
Đọc tiếp
Chứng minh định lí: “Nếu hai đường thẳng xx’, yy’ cắt nhau tại O và góc xOy vuông thì các góc đều là góc vuông”.
13 tháng 11 2021 lúc 17:12
Cho hai đường thẳng xx’ và yy’ cắt nhau tại O. Biết số đo góc xOy bằng 5 lần số đo góc x’Oy. Số đo góc x’Oy’ là:
A. 150\(^o\)
B. 45\(^o\)
. C. 30\(^o\) .
D. 60\(^o\)
Ta có \(\widehat{xOy}+\widehat{x'Oy}=180^0\) (kề bù)
\(\Rightarrow5\widehat{x'Oy}+\widehat{x'Oy}=180^0\\ \Rightarrow6\widehat{x'Oy}=180^0\\ \Rightarrow\widehat{x'Oy}=30^0\\ \Rightarrow\widehat{xOy}=150^0\)
Vậy \(\widehat{x'Oy'}=\widehat{xOy}=150^0\) (đối đỉnh)
Chọn A
Đúng 2
Bình luận (1)
Xem thêm câu trả lời