Cho hàm số y = f ( x ) = 3 x + 4 x , khẳng định nào sau đây là sai?
A. Phương trình ![]() có duy nhất nghiệm
có duy nhất nghiệm
B. ![]() luôn đồng biến trên
luôn đồng biến trên ![]()
C. Phương trình ![]() vô nghiệm
vô nghiệm
D. Phương trình ![]() có hai nghiệm phân biệt
có hai nghiệm phân biệt
Câu4 :Cho hàm số y = f(x) = 2x. Khẳng định nào sau đây đúng? A. f(0) = 0 B. f(1) = 6 C. f(-1) = 10 D. f(2) = -4 Câu 5:Một hàm số được cho bẳng công thức y = f(x) = x2 ( x bình phương) Khẳng định nào sau đây đúng? A. f(1) = 6 Câu6:Cho hàm số y = f(x) = 2 + 8x. Khẳng định nào sau đây đúng? A. f(0) = 0 B. f(1) = 10 C. f(-1) = 10 D. f(2) = -4 Câu7:Một hàm số được cho bẳng công thức y = f(x) = 2x. Tính f(-5) + f(5). KẾT QUẢ ĐÚNG LÀ A. 0 B. 25 C. 50 D. 10
Cho hàm số y = f(x) có lim x → + ∞ f ( x ) = 3 và lim x → - ∞ f ( x ) = - 3 Khẳng định nào sau đây là khẳng định đúng?
A. Đồ thị hàm số đã cho có đúng một tiệm cận ngang
B. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng x = 3 và x = -3
C. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng y = 3 và y = -3
D. Đồ thị hàm số đã cho không có tiệm cận ngang
Đáp án C.
Ta có: ![]()
=> y = 3, y = -3 là hai tiệm cận ngang.
Cho hàm số y = f(x) có lim x → + ∞ f ( x ) = 3 và lim x → - ∞ f ( x ) = - 3 . Khẳng định nào sau đây là khẳng định đúng:
A. Đồ thị hàm số đã cho không có tiệm cận ngang
B. Đồ thị hàm số đã cho có đúng một tiệm cận ngang
C. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng y = 3 và y = -3
D. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng x = 3 và x = -3
Đáp án C.
![]() => đồ thị hàm số có hai tiệm cận ngang y = ±3
=> đồ thị hàm số có hai tiệm cận ngang y = ±3
Cho hàm số y = f ( x ) . Hàm số y = f ' ( x ) có đồ thị như hình vẽ:
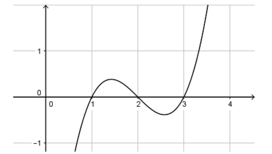
Khẳng định nào sau đây là khẳng định đúng?
A. Đồ thị hàm số y = f ( x ) cắt trục hoành tại ba điểm phân biệt
B. Đồ thị hàm số y = f ( x ) có hai điểm cực trị
C. Đồ thị hàm số y = f ( x ) có ba điểm cực trị
D. Đồ thị hàm số y = f ( x ) có một điểm có một điểm cực trị
Cho hàm số y = f ( x ) . Hàm số y = f ' ( x ) có đồ thị như hình vẽ
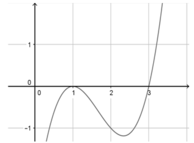
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số y = f ( x ) đạt cực đại tại x = 1
B. Đồ thị hàm số y = f ( x ) có một điểm cực tiểu
C. Hàm số y = f ( x ) đồng biến trên ( - ∞ ; 1 )
D. Đồ thị hàm số y = f ( x ) có hai điểm cực trị
Cho hàm số y = f(x) = x + 3. Khẳng định nào sau đây sai?
A. f(1) = 4 . B. f(0) = 3. C. f(–1) = 4. D. f(5) = 8.
Cho hàm số y = f(x) xác định trên M và có đạo hàm f ' ( x ) = x + 2 x - 1 2 Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số ![]() đồng biến trên
đồng biến trên ![]()
B. Hàm số ![]() đạt cực đại tại
đạt cực đại tại ![]()
C. Hàm số ![]() đạt cực đại tiểu
đạt cực đại tiểu ![]()
D. Hàm số ![]() nghịch biến trên
nghịch biến trên ![]()
Cho hàm số y=f(x) xác định trên ℝ và có đồ thị của hàm số f'(x), biết f(3)+f(20=f(0)+f(1) và các khẳng định sau:
1) Hàm số y=f(x) có 2 điểm cực trị
2) Hàm số y=f(x) đồng biến trên khoảng - ∞ ; 0
3) M a x 0 ; 3 f x = f 3
4) M a x ℝ f x = f 2
5) M a x - ∞ ; 2 f x = f 0 .
Số khẳng định đúng là

A. 2
B. 3
C. 4
D. 5
Cho hàm số y = f ( x ) = x - 2 3 - x . Khẳng định nào sau đây là khẳng định đúng ?
A. Đồ thị của hàm số đã cho có đường tiệm cận đứng x=-1 và một tiệm cận ngang y=3.
B. Đồ thị của hàm số đã cho có đường tiệm cận đứng x=3 và một tiệm cận ngang y=-1.
C. Đồ thị của hàm số đã cho có đường tiệm cận đứng x=-1
D. Đồ thị của hàm số đã cho có một đường tiệm cận ngang là y=3
Đáp án B
Ta có: lim x → ± ∞ x - 2 - x + 3 = - 1 suy ra TCN: y=-1
lim x → 3 + x - 2 - x + 3 = - ∞ , lim x → 3 - x - 2 - x + 3 = + ∞ suy ra TCĐ: x=3
Cho hàm số y = f(x) thỏa mãn f’(x) = x2 – 5x +4. Khẳng định nào sau đây là đúng?
A. Hàm số đã cho đồng biến trên khoảng - ∞ ; 3
B. Hàm số đã cho nghịch biến trên khoảng 3 ; + ∞
C. Hàm số đã cho nghịch biến trên khoảng (2;3)
D. Hàm số đã cho đồng biến trên khoảng (1;4)
Đáp án C
Phương pháp giải: Lập bảng xét dấu y’ để tìm khoảng đơn điệu của hàm số
Lời giải:
Ta có f’(x) = x2 – 5x +4 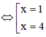 suy ra
suy ra 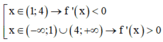
Do đó, hàm số nghịch biến trên khoảng (1;4) và đồng biến trên khoảng - ∞ ; 1 và 4 ; + ∞
Vì (2;3) ⊂ (1;4) suy ra hàm số đã cho nghịch biến trên khoảng (2;3)