a: Để (1) là hàm số bậc nhất thì \(m-2\ne0\)

=>\(m\ne2\)

b: Để (1) đồng biến thì m-2>0

=>m>2

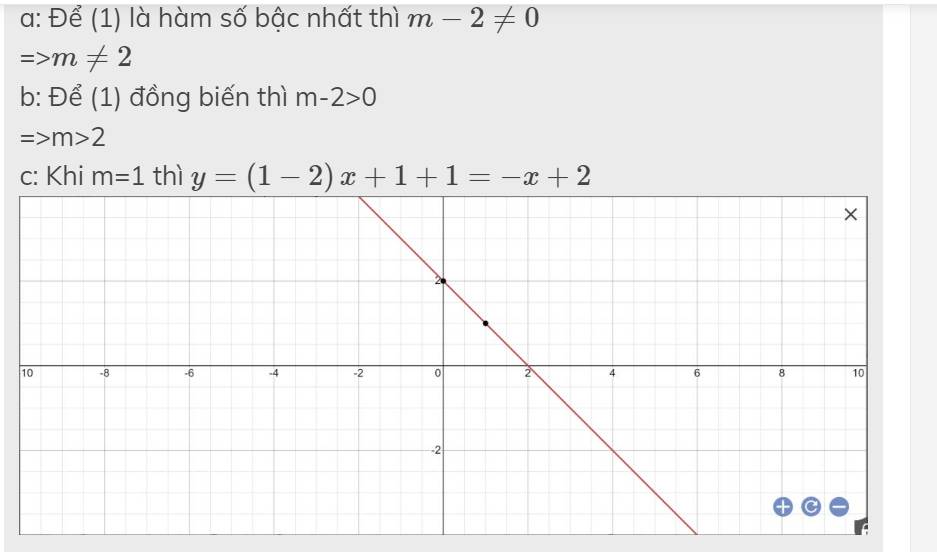
c: Khi m=1 thì \(y=\left(1-2\right)x+1+1=-x+2\)

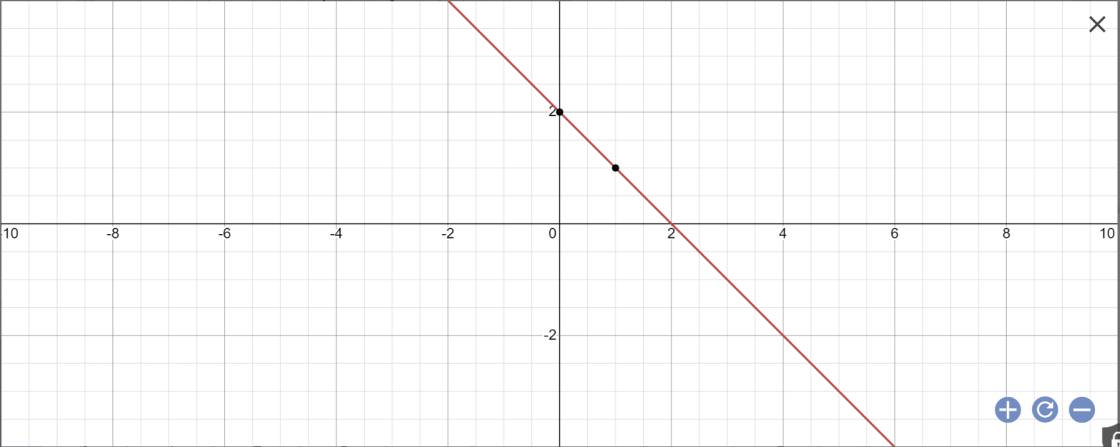
d: Thay x=2 và y=1 vào (1), ta được:

\(2\left(m-2\right)+m+1=1\)

=>2m-4+m=0

=>3m-4=0

=>3m=4

=>\(m=\dfrac{4}{3}\)

e: Để (1)//y=3x+2 thì \(\left\{{}\begin{matrix}m-2=3\\m+1< >2\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}m=3\\m< >1\end{matrix}\right.\)

=>m=3

f: Để (1) tạo với trục Ox một góc tù thì m-2<0

=>m<2

g: Thay x=0 vào y=5x+6, ta được:

\(y=5\cdot0+6=6\)

Thay x=0 và y=6 vào (1), ta được:

\(0\left(m-2\right)+m+1=6\)

=>m+1=6

=>m=5

h: Khi m=3 thì \(y=\left(3-2\right)x+3+1=x+4\)

Gọi \(\alpha\) là góc tạo bởi đồ thị hàm số y=x+4 với trục Ox

\(tan\alpha=a=1\)

=>\(\alpha=45^0\)

y=x+4

=>x-y+4=0

Khoảng cách từ O(0;0) đến đường thẳng x-y+4=0 là:

\(\dfrac{\left|0\cdot1+0\cdot\left(-1\right)+4\right|}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{4}{\sqrt{2}}=2\sqrt{2}\)

Hàm số y = ( k + 1)x + 3 có các hệ số a = k + 1, b = 3

Hàm số y = (3 – 2k)x + 1 có các hệ số a' = 3 - 2k, b' = 1

Hai hàm số là hàm số bậc nhất nên a và a' khác 0, tức là:

a) Theo đề bài ta có b ≠ b' (vì 3 ≠ 1)

Nên hai đường thẳng y = (k + 1)x + 3 và y = (3 – 2k)x + 1 song song với nhau khi a = a'

tức là: k + 1 = 3 – 2k

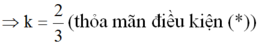
b) Hai đường thẳng y = (k + 1)x + 3 và y = (3 – 2k)x + 1 là hàm số bậc nhất nên a ≠ 0 và a' ≠ 0. Hai đường thẳng này cắt nhau khi a ≠ a' tức là:

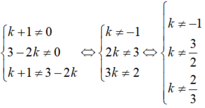
Vậy với  thì đồ thị của hai hàm số trên là hai đường thẳng cắt nhau.

c) Do b ≠ b' (vì 3 ≠ 1) nên hai đường thẳng không thể trùng nhau với mọi giá trị k.

a: Để hai đường thẳng song song thì m-1=3-m

=>2m=4

hay m=2

\(\text{//}\Leftrightarrow m-1=3-m\Leftrightarrow m=2\\ \cap\Leftrightarrow m-1\ne3-m\Leftrightarrow m\ne2\)

a) H/s là bậc nhất ⇔ m+5≠0 ⇔m ≠-5

b)  H/s đồng biến ⇔ m+5> 0 ⇔ m> -5

c)  H/s đi qua A( 2,3)    ⇔  2=(m+5).2 +2m -10    ⇔ 2m+ 2m +10 -10 =2

                                     ⇔ m= \(\dfrac{1}{2}\)

d) H/s cắt trục tung tại điểm có tung độ bằng 9

⇔ x=0 thì y=9       ⇔ (m+5).0 +2m -10 =9

                             ⇔m= \(\dfrac{19}{2}\)

e) H/s đi qua điểm 10 trên trục hoành ⇔ y=0, x=10 

⇔ 0= (m+5).10 +2m -10      ⇔m= \(\dfrac{-40}{12}\)

f) h/s song song với y=2x-1 

⇔ \(\left\{{}\begin{matrix}m+5=2\\2m-10\ne-1\end{matrix}\right.\)

⇔\(\left\{{}\begin{matrix}m=-3\\m\ne\dfrac{9}{2}\end{matrix}\right.\)

⇔m=-3

\(a,\Leftrightarrow\dfrac{m-1}{m+1}\ne0\Leftrightarrow m\ne\pm1\\ b,\Leftrightarrow\dfrac{m-1}{m+1}>0\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -1\end{matrix}\right.\\ c,\Leftrightarrow\dfrac{m-1}{m+1}+m+2=2\\ \Leftrightarrow\dfrac{m-1+m^2+m}{m+1}=0\\ \Leftrightarrow m^2+2m-1=0\\ \Leftrightarrow\left[{}\begin{matrix}m=-1+\sqrt{2}\\m=-1-\sqrt{2}\end{matrix}\right.\)

a: Để hàm số y=(m-1)x+3 đồng biến trên R thì m-1>0

=>m>1

Để hàm số y=(m-1)x+3 nghịch biến trên R thì m-1<0

=>m<1

b: Thay m=3 vào (d), ta được:

\(y=\left(3-1\right)x+3=2x+3\)

Vẽ đồ thị:

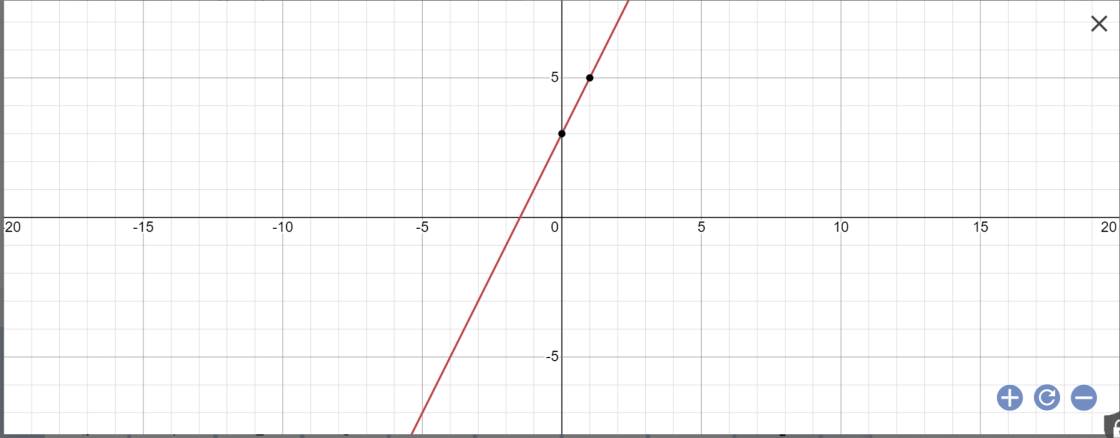
c: Để (d1)//(d2) thì \(\left\{{}\begin{matrix}m-1=2\\3\ne-1\left(đúng\right)\end{matrix}\right.\)

=>m-1=2

=>m=3

d: Thay x=-2 và y=0 vào (d1), ta được:

\(-2\left(m-1\right)+3=0\)

=>-2(m-1)=-3

=>\(m-1=\dfrac{3}{2}\)

=>\(m=\dfrac{3}{2}+1=\dfrac{5}{2}\)