Cho a, b là các số thực dương, khác 1. Đặt log a b = α Biểu thức P = log a 2 b - log b a 3 là:
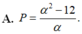
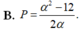
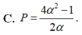

Cho a, b là các số thực dương, khác 1. Đặt log a b = α . Biểu thức P = log a 2 b - log b a 3 là:
A. P = a 2 - 12 α
B. P = a 2 - 12 2 α
C. P = 4 a 2 - 1 2 α
D. P = a 2 - 2 2 α
Cho a,b,c là các số thực dương thỏa mãn a log 5 2 = 4 , b log 4 6 = 1 , log , c log 7 3 = 49 Tính giá trị của biểu thức T = a log 2 2 5 + b log 4 2 6 + 3 c log 7 2 3
A. T=126
B. T = 5 + 2 3
C. T=88
D. T = 3 - 2 3
Cho số dương a khác 1 và các số thực α ; β . Đẳng thức nào sau đây là sai?
A. a α . a β = a α . β
B. a α . a β = a α + β
C. a α β = a α . β
D. a α a β = a α - β
Cho số dương a khác 1 và các số thực α , β . Đẳng thức nào sau đây là sai?
A. a α . a β = a α . β
B. a α . a β = a α + β
C. a α β = a α . β
D. a α a β = a α − β
Đề bài
Cho hai số thực dương a, b thỏa mãn \({a^3}{b^2} = 100\). Tính giá trị của biểu thức \(P = 3\log a + 2\log b\)
\(P=loga^3+logb^2=log\left(a^3b^2\right)=log\left(100\right)=10\)
1) Cho a,b là các số thực dương khác 1 và thoả mãn ab khác 1. Rút gọn biểu thức sau: P=(logab + logba + 2)(logab - logabb).logba - 1
Cho a, b là các số thực dương thỏa mãn log 2 a + log 2 b = 0.
Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số lôgarit \(y = {\log _a}x;\,y = {\log _b}x;\,y = {\log _c}x\) được cho bởi Hình 15. Kết luận nào sau đây là đúng với ba số a, b, c?
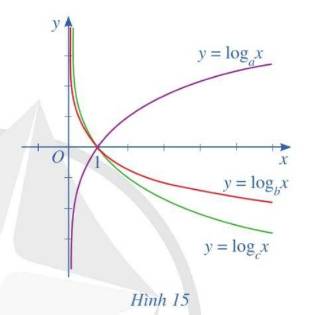
A. c < a < b
B. c < b < a
C. a < b < c
D. b < c < a
Cho các số thực dương a,b thỏa mãn log a = x , log b = y . Tính P = log ( a 2 b 3 )
![]()
![]()
![]()
![]()