Xét các số thực a, b thỏa mãn a ≥ b > 1 . Biết rằng biểu thức P = 1 log a b a + log a a b đạt giá trị lớn nhất khi b = ak. Khẳng định nào sau đây đúng?
![]()
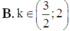
![]()
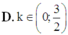
Xét các số thực a, b thỏa mãn a ≥ b > 1. Biết rằng biểu thức P = 1 log a b a + log a a b đạt giá trị lớn nhất khi b = a k . Khẳng định nào sau đây đúng?
A. k ∈ 2 ; 3
B. k ∈ 3 2 ; 2
C. k ∈ − 1 ; 0
D. k ∈ 0 ; 3 2
Đáp án D
Đặt 0 < t = log a b ≤ 1
⇒ P = log a a b + log a a + log a b = 1 + t + 1 − t = f t
f ' t = 1 − 1 2 1 − t → f ' t = 0
⇔ t = 3 4 ⇒ f 3 4 = 9 4 .
Dựa vào bảng biến thiên,
suy ra f t 0 < t ≤ 1 ≤ f 3 4
Khi đó t = 3 4 = log a b
⇔ a 3 4 = b ⇔ k = 3 4
Xét các số thực a, b thỏa mãn a > b > 1. Tìm giá trị nhỏ nhất của biểu thức P = log a b 2 a 2 + 3 log b a b .
A. P min = 19.
B. P min = 13.
C. P min = 14.
D. P min = 15.
Xét các số thực a, b thỏa mãn b>1 và a ≤ b < a Biểu thức P = log a b a + 2 log b a b đạt giá trị nhỏ nhất khi
A . a = b 2
B . a 2 = b 3
C . a 3 = b 2
D . a 2 = b
Xét các số thực a, b thỏa mãn a > b > 1 . Tìm giá trị nhỏ nhất của biểu thức P = log a b 2 a 2 + 3 log b a b
A. P m i n = 19
B. P m i n = 13
C. P m i n = 14
D. P m i n = 15
Xét các số thực a, b thỏa mãn a> b > 1. Tìm giá trị nhỏ nhất của biểu thức P = log a b 2 ( a 2 ) + 3 log b a b
A. P m i n = 19
B. P m i n = 13
C. P m i n = 14
D. P m i n = 15
Xét các số thực a; b thỏa mãn a> b> 1 . Tìm giá trị nhỏ nhất Pmin của biểu thức P = log 2 a b a 2 + 3 log b a b
A. 19
B. 13
C. 14
D. 15
Ta có:
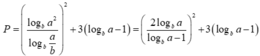
Đặt t= logba-1 > logbb -1=0 ,
khi đó:
P = 2 t + 2 t 2 + 3 t = f ( t ) f ' t = 2 . 2 t + 2 t . - 2 t 2 + 3 = 3 t 3 - 8 ( t + 1 ) t 3
F’ (t) =0 khi 3t3-8( t+1) =0 hay t= 2.
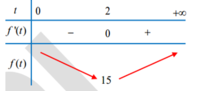
Suy ra Pmin =f(2) =15
Chọn D.
Xét các số thực a, b thỏa mãn 1 4 < b < a < 1 Biểu thức P = log a ( b - 1 4 ) - log a b b đạt giá trị nhỏ nhất khi
A. log a b = 1 3
B. log a b = 2 3
C. log a b = 3 2
D. log a b = 3
Xét các số thực a; b thỏa mãn a > b > 1 Tìm giá trị nhỏ nhất Pmin của biểu thức P = log a b 2 a 2 + 3 log b a b
A.19
B.13
C.14
D.15
xét các số thực dương a,b thỏa mãn a+b=2. Tìm max của biểu thức P=a^2*b
Lời giải:
Áp dụng BĐT Cô-si:
\(2=a+b=\frac{a}{2}+\frac{a}{2}+b\geq 3\sqrt[3]{\frac{a^2b}{4}}\)
\(\Rightarrow \frac{2}{3}\geq \sqrt[3]{\frac{a^2b}{4}}\Rightarrow \frac{8}{27}\geq \frac{a^2b}{4}\)
\(\Leftrightarrow a^2b\leq \frac{32}{27}\Leftrightarrow P\leq \frac{32}{27}\)
Vậy $P_{\max}=\frac{32}{27}$. Giá trị này đạt tại $\frac{a}{2}=b=\frac{2}{3}$