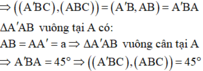Cho hình lăng trụ đứng có AB = a, AC = 2a, A A 1 = 2 a 5 và B A C ^ = 120 0 . Gọi K, I lần lượt là trung điểm của các cạnh C C 1 , B B 1 . Khoảng cách từ điểm I đến mặt phẳng A 1 B K bằng
![]()

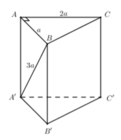
Cho hình lăng trụ đứng \(ABCD.A'B'C'D'\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(B\), \(AA' = 2a,AD = 2a,AB = BC = a\).
a) Tính độ dài đoạn thẳng \(AC'\).
b) Tính tổng diện tích các mặt của hình lăng trụ.
a) \(\Delta ABC\) vuông cân tại \(B \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \)
\(CC' = AA' = 2a\)
\(CC' \bot \left( {ABCD} \right) \Rightarrow CC' \bot AC\)
\( \Rightarrow \Delta ACC'\) vuông tại \(C \Rightarrow AC' = \sqrt {A{C^2} + CC{'^2}} = a\sqrt 6 \)
b) \({S_{ABC{\rm{D}}}} = {S_{A'B'C'C'}} = \frac{1}{2}\left( {A{\rm{D}} + BC} \right).AB = \frac{{3{a^2}}}{2}\)
Gọi \(M\) là trung điểm của \(AD\)
\( \Rightarrow ABCM\) là hình vuông\( \Rightarrow MC = M{\rm{D}} = MA = \frac{1}{2}A{\rm{D}} = a\)
\(\Delta MC{\rm{D}}\) vuông cân tại \(M \Rightarrow C{\rm{D}} = \sqrt {C{M^2} + D{M^2}} = a\sqrt 2 \)
\(\begin{array}{l}{S_{ABB'A'}} = AB.AA' = 2{a^2}\\{S_{ADD'A'}} = AD.AA' = 4{a^2}\\{S_{BCC'B'}} = BC.CC' = 2{a^2}\\{S_{C{\rm{DD}}'{\rm{C}}'}} = C{\rm{D}}.CC' = 2{a^2}\sqrt 2 \end{array}\)
Tổng diện tích các mặt của hình lăng trụ là:
\(\begin{array}{l}S = {S_{ABC{\rm{D}}}} + {S_{A'B'C'C'}} + {S_{ABB'A'}} + {S_{ADD'A'}} + {S_{BCC'B'}} + {S_{C{\rm{DD}}'{\rm{C}}'}}\\ & = \frac{{3{a^2}}}{2} + \frac{{3{a^2}}}{2} + 2{a^2} + 4{a^2} + 2{a^2} + 2{a^2}\sqrt 2 = \left( {11 + 2\sqrt 2 } \right){a^2}\end{array}\)
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A, biết AB = a, AC = 2a và A'B = 3a. Tính thể tích của khối lăng trụ ABC.A'B'C'
A. 5 a 3 3
B. 5 a 3
C. 2 2 a 3
D. 2 2 a 3 3
Phương pháp:
Sử dụng công thức tính thể tích lăng trụ V = S đ á y . h
Cách giải:
Trong tam giác vuông A'AB có:
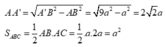
Vậy ![]()
Chọn: C
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A, biết A B = a , A C = 2 a , và A ' B = 3 a . Tính thể tích của khối lăng trụ ABC.A'B'C'
A. 5 a 3 3
B. 5 a 3
C. 2 2 a 3
D. 2 2 a 3 3
Cho hình lăng trụ đứng ABC.A'B'C' có tam giác ABC vuông tại A, A B = A A ' = a , A C = 2 a . Tính thể tích khối lăng trụ đã cho
A. a 3 3
B. 2 a 3 3
C. a 3
D. 2 a 3
Đáp án C
Thể tích khối lăng trụ là: V = A A ' . S A B C = a . 1 2 a .2 a = a 3
Cho hình lăng trụ đứng ABC.A’B’C’ có tam giác ABC vuông tại A, AB = AA’ = a, AC = 2a. Tính thể tích khối lăng trụ đã cho.
![]()
B. a3
C. 2a3
![]()
Cho hình lăng trụ đứng ABC. A’B’C’ có tam giác ABC vuông tại A, AB= AA’=a, AC =2a . Tính thể tích khối lăng trụ đã cho
A. a 3 3
B. 2 a 3 3
C. a 3
D. 2 a 3
Cho hình lăng trụ đứng ABC.A' B' C' có đáy ABC là tam giác vuông tại A, biết AB = a, AC = 2a và A' B = 3a. Tính thể tích của khối lăng trụ ABC.A' B' C'.
A. 2 2 a 3
B. 5 a 3 3
C. 2 2 a 3 3
D. 5 a 3
Chọn A.
Phương pháp
Tính diện tích tam giác đáy và chiều cao lăng trụ suy ra thể tích theo công thức V=Bh .
Cách giải:
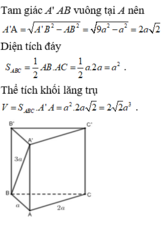
Cho hình lăng trụ đứng ABC.A' B' C' có đáy ABC là tam giác vuông tại A, biết AB = a, AC = 2a và A' B = 3a. Tính thể tích của khối lăng trụ ABC.A' B' C'.
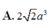
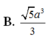
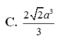
![]()
Cho lăng trụ đứng ABC.A'B'C' có AB=AA'=a, BC=2a, AC=a 5 . Tính góc giữa hai mặt phẳng (ABC) Và (A'BC).
A. 45 o
B. 60 o
C. 30 o
D. 135 o
Cho hình lăng trụ đứng ABC.A'B'C' có AB = AA ' = a , BC = 2 a , AC = a 5 . Tính góc giữa hai mặt phẳng (ABC) và (A'BC)
A. 45 °
B. 60 °
C. 30 °
D. 135 °
Đáp án A
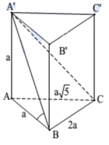

Và BC là giao tuyến của (A'BC) và (ABC)