Phương pháp:
Sử dụng công thức tính thể tích lăng trụ V = S đ á y . h
Cách giải:
Trong tam giác vuông A'AB có:
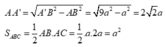
Vậy ![]()
Chọn: C
Phương pháp:

Sử dụng công thức tính thể tích lăng trụ V = S đ á y . h
Cách giải:
Trong tam giác vuông A'AB có:
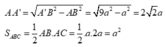
Vậy ![]()
Chọn: C
Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác vuông cân tại B, AB = a, A'B=a 3 . Thể tích khối lăng trụ ABC.A'B'C' bằng:
A. a 3 3 2
B. a 3 6
C. a 3 2
D. a 3 2 2
a) Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, AB=a. Biết diện tích tứ giác ABB'A' bằng \(2a^2\), thể tích khối lăng trụ ABC.A'B'C' bằng?
b) Cho hình lăng trụ đúng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, AB=a. Biết góc giữa (AB'C') và (A'B'C') bằng 60°, thể tích khối lăng trụ ABC.A'B'C' bằng?
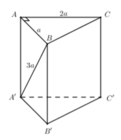
Lăng trụ tam giác ABC.A'B'C' có tam giác ABC vuông tại A; AB = a 3 ; BC = 2a. Biết AA' = A'B = A'C = a 3 . Tính thể tích V của hình lăng trụ.
A. V = a 3 2 3
B. V = a 3 6 3
C. V = a 3 6 2
D. V = a 3 2
Lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A; AB=AC=a 5 ; A'B tạo với mặt đáy lăng trụ góc 60 0 . Thể tích khối lăng trụ bằng:
![]()
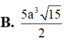
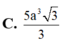
![]()
Cho khối lăng trụ tam giác đứng ABC.A'B'C' có đáy là tam giác vuông tại A, AC = AB = 2a, góc giữa AC' và mặt phẳng (ABC) bằng 300. Tính thể tích của khối lăng trụ ABC.A'B'C'
A. 2 3 a 3 3
B. 3 a 3 3
C. a 3 3
D. 4 3 a 3 3
Cho khối lăng trụ tam giác đứng ABC.A'B'C' có đáy là tam giác vuông tại A, AC = AB = 2a, góc giữa AC' và mặt phẳng (ABC) bằng 300. Tính thể tích của khối lăng trụ ABC.A'B'C'.
A. 2 3 a 3 3
B. 3 a 3 3
C. a 3 3
D. 4 3 a 3 3
Cho khối lăng trụ đứng tam giác ABC.A'B'C' có đáy ABC là tam giác vuông tại A, AB=a, AC=a 3 , AA'=2a. Tính bán kính R của mặt cầu ngoại tiếp khối lăng trụ đó.
![]()
![]()
![]()
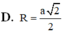
Cho lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều cạnh a 3 , A'B=3a. Thể tích khối lăng trụ đã cho là:
A. 9 2 a 3 4
B. 7 a 3 2
C. 6 a 3
D. 7 a 3
Lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, AB =AC = a 5 , A'B tạo với mặt đáy lăng trụ góc 600. Tính thể tích khối lăng trụ.
A. a 3 6
B. 5 a 3 15 2
C. 5 a 3 3 3
D. 4 a 3 6