Bài 1: Cho ABC cân tại A. Gọi E, F, H lần lượt là trung điểm của AB, AC, BC.
a) Chứng minh AE = AF.
b) Chứng minh AEHF là hình thoi.

Những câu hỏi liên quan
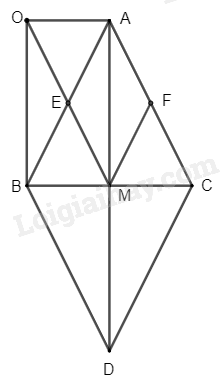
Cho tam giác ABC cân tại A, gọi M là trung điểm của BC. Lấy điểm D đối xứng với điểm A qua BC.
a) Chứng minh tứ giác ABDC là hình thoi
b) Gọi E, F lần lượt là trung điểm của AB và AC, lấy điểm O sao cho E là trung điểm của OM. Chứng minh rằng hai tam giác AOB và MBO bằng nhau
c) Chứng minh tứ giác AEMF là hình thoi
a) Xét tứ giác \(ABDC\) có:
\(M\) là trung điểm của \(BC\) (gt)
\(M\) là trung điểm của \(AD\) (do \(D\) đối xứng với \(A\) qua \(BC\))
Suy ra \(ABDC\) là hình bình hành
b) Do \(\Delta ABC\) cân tại \(A\), có \(AM\) là trung tuyến (gt)
Suy ra \(AM\) là đường cao, trung trực, phân giác
Suy ra \(AM\) vuông góc \(BM\) và \(CM\)
Xét tứ giác \(OAMB\) ta có:
\(E\) là trung điểm của \(OM\) và \(AB\) (gt)
Suy ra \(OAMB\) là hình bình hành
Suy ra \(OB\) // \(AM\); \(OA\) // \(MB\); \(OA = BM\); \(OB = AM\)
Mà \(AM \bot BM\) (cmt)
Suy ra: \(AM \bot OA\); \(OB \bot MB\)
Mà \(AM\) // \(OB\) (cmt)
Suy ra \(OB \bot OA\)
Xét \(\Delta AOB\) và \(\Delta MBO\) (các tam giác vuông) ta có:
\(\widehat {{\rm{AOB}}} = \widehat {{\rm{OBM}}} = 90^\circ \)
\(AO = MB\) (cmt)
\(OB = AM\) (cmt)
Suy ra \(\Delta AOB = \Delta MBO\) (c-g-c)
Suy ra \(OM = AB\)
c) \(OM = AB\) (cmt)
Mà \(EM = EO = \frac{1}{2}OM\); \(EA = EB = \frac{1}{2}AB\)
Suy ra \(EO = EA = EM = EB\) (1)
Xét \(\Delta ABC\) cân ta có: \(\widehat {{\rm{ABC}}} = \widehat {{\rm{ACB}}}\) và \(AB = AC\)
Mà \(EA = EB = \frac{1}{2}AB\); \(FA = FC = \frac{1}{2}AC\) (gt)
Suy ra \(AE = EB = FA = FM\) (2)
Xét \(\Delta BEM\) và \(\Delta CMF\) ta có:
\(BE = CF\) (cmt)
\(\widehat {{\rm{ABC}}} = \widehat {{\rm{ACB}}}\) (cmt)
\(BM = CM\) (gt)
Suy ra \(\Delta BEM = \Delta CFM\) (c-g-c)
Suy ra \(EM = FM\) (3)
Từ (1), (2), (3) suy ra \(AE = AF = FM = ME\)
Suy ra \(AEMF\) là hình thoi
Đúng 0
Bình luận (0)
a) Cho ∆ABC vuông tại A có đường cao AH. Gọi E, F lần lượt là hình chiếu của H
trên AB, AC. Chứng minh AEHF là hình chữ nhật.
b) Cho ∆ABC vuông tại A. Gọi M là trung điểm BC. Vẽ D là điểm đối xứng với A
qua M. Chứng minh ABDC là hình chữ nhật.
a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
Do đó: AEHF là hình chữ nhật
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC cân tại A. Gọa D, E, F lần lượt là trung điểm của AB, AC, BC. Chứng minh tứ giác ADFE là hình thoi.
Xét ΔABC có
F là trung điểm của BC
E là trung điểm của AC
Do đó: FE là đường trung bình của ΔABC
Suy ra: FE//AB và \(FE=\dfrac{AB}{2}\)
hay FE//AD và FE=AD
Ta có: \(AD=\dfrac{AB}{2}\)
\(AE=\dfrac{AC}{2}\)
mà AB=AC
nên AD=AE
Xét tứ giác ADFE có
FE//AD
FE=AD
Do đó: ADFE là hình bình hành
mà AD=AE
nên ADFE là hình thoi
Đúng 2
Bình luận (0)
cho tam giác ABC vuông tại A . có đường ca AH (H thuộc BC). E và F lần lượt là hình chiếu của H trên AB , AC
a) chứng minh AEHF là hình chữ nhật
b) Gọi I và K lần lượt là trung điểm của HB và BC . chứng minh IE song song KF
Bài 4. (3,0 điểm) Cho tam giác ABC vuông tại A đường cao AH. Gọi E, F lần lượt
kė tur H den AB, AC. a) Tứ giác AEHF là hình gì? Vì sao?
b) Gọi I là trung điểm của BC, K đối xứng với A qua I. Chứng minh BC c) Chứng minh AI LEF
Cho tam giác ABC vuông tại A đường cao AH. Gọi E,F lần lượt kẻ từ H dến AB và AC. a) Tứ giác AEHF là hình gì? Vì sao?.b) Gọi I là trung điểm của BC, K đối xứng với A qua I. Chứng minh BCAK.c) Chứng minh AI vuông góc với EF
Đọc tiếp
Bài 4. (3,0 điểm) Cho tam giác ABC vuông tại A đường cao AH. Gọi E, F lần lượt kė tur H den AB, AC. a) Tứ giác AEHF là hình gì? Vì sao? b) Gọi I là trung điểm của BC, K đối xứng với A qua I. Chứng minh BC = c) Chứng minh AI LEF Cho tam giác ABC vuông tại A đường cao AH. Gọi E,F lần lượt kẻ từ H dến AB và AC. a) Tứ giác AEHF là hình gì? Vì sao?.b) Gọi I là trung điểm của BC, K đối xứng với A qua I. Chứng minh BC=AK.c) Chứng minh AI vuông góc với EF
a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
Do đó:AEHF là hình chữ nhật
Đúng 0
Bình luận (0)
Bài 1: Cho tứ giác ABCD có BC AD và BC không song song với AD, gọi M, N,P, Q, E, F lần lượt là trung điểm của các đoạn thẳng AB, BC, CD, DA, AC, BD.a) Chứng minh tứ giác MEPF là hình thoi.b) Chứng minh các đoạn thẳng MP, NQ, EF cùng cắt nhau tại một điểm.c) Tìm thêm điều kiện của tứ giác ABCD để N, E, F, Q thẳng hàngBài 2: Cho tam giác ABC vuông tại A (AB<AC), M là trung điểm BC, từ M kẻđường thẳng song song với AC, AB lần lượt cắt AB tạt E, cắt AC tại Fa) Chứng minh EFCB là hình thangb) Chứ...
Đọc tiếp
Bài 1: Cho tứ giác ABCD có BC = AD và BC không song song với AD, gọi M, N,
P, Q, E, F lần lượt là trung điểm của các đoạn thẳng AB, BC, CD, DA, AC, BD.
a) Chứng minh tứ giác MEPF là hình thoi.
b) Chứng minh các đoạn thẳng MP, NQ, EF cùng cắt nhau tại một điểm.
c) Tìm thêm điều kiện của tứ giác ABCD để N, E, F, Q thẳng hàng
Bài 2: Cho tam giác ABC vuông tại A (AB<AC), M là trung điểm BC, từ M kẻ
đường thẳng song song với AC, AB lần lượt cắt AB tạt E, cắt AC tại F
a) Chứng minh EFCB là hình thang
b) Chứng minh AEMF là hình chữ nhật
c) Gọi O là trung điểm AM. Chứng minh: E và F đối xứng qua O.
d) Gọi D là trung điểm MC. Chứng minh: OMDF là hình thoi
Bài 3: Cho tam giác ABC có AB<AC. Gọi M, N, P lần lượt là trung điểm của AB,
AC, BC. Vẽ đường cao AH của tam giác ABC. Tứ giác HMNP là hình gì.
Bài 4: Cho tứ giác ABCD có góc DAB = góc BCD = 120 0 . Tính số đo của hai góc
còn lại để ABCD là hình bình hành.
Bài 5: Cho hình bình hành ABCD. Trên đưởng chéo AC chọn hai điểm E và F sao
cho AE=EF=FC.
a) Tứ giác BEDF là hình gì?
b) Chứng minh CFDAEB .
c) Chứng minh CFBEAD .
Bài 6: Cho tam giác ABC cân tại A, đường cao AD. Gọi E là điểm đối xứng với D qua
trung điểm M của AC.
a) Tứ giác ADCE là hình gì? Vì sao?
b) Tứ giác ABDM là hình gì? Vì sao?
c) Tam giác ABC có thêm điều kiện gì thì ADCE là hình vuông?
d) Tam giác ABC có thêm điều kiện gì thì ABDM là hình thang cân?
Bài 1:
a) Xét tam giác ABC có M là trung điểm của AB (gt) ,E là trung điểm của AC (gt)
\(\Rightarrow ME\)là đường trung bình tam giác ABC
\(\Rightarrow ME=\frac{1}{2}BC\left(tc\right)\left(1\right)\)
Xét tam giác ADC có E là trung điểm của AC (gt) ,P là trung điểm của DC (gt)
\(\Rightarrow PE\)là đường trung bình của tam giác ADC
\(\Rightarrow PE=\frac{1}{2}AD\left(tc\right)\left(2\right)\)
mà \(AD=BC\left(gt\right)\left(3\right)\)
Từ (1) , (2) và (3) \(\Rightarrow EM=PE\)
CMTT: \(PE=FP,FM=ME\)
\(\Rightarrow ME=EP=PF=FM\)
Xét tứ giác MEPF có:
\(ME=EP=PF=FM\left(cmt\right)\)
\(\Rightarrow MEPF\)là hình thoi ( dhnb)
b) Vì \(MEPF\)là hình thoi (cmt)
\(\Rightarrow FE\)giao với MP tại trung điểm mỗi đường (tc) (4)
Xét tam giác ADB có M là trung điểm của AB(gt) ,Q là trung điểm của AD (gt)
\(\Rightarrow MQ\)là đường trung bình của tam giác ADB
\(\Rightarrow MQ//DB,MQ=\frac{1}{2}DB\left(tc\right)\left(5\right)\)
Xét tam giác BDC có N là trung điểm của BC(gt) , P là trung điểm của DC(gt)
\(\Rightarrow NP\)là đường trung bình của tam giác BDC
\(\Rightarrow NP//DB,NP=\frac{1}{2}DB\left(tc\right)\left(6\right)\)
Từ (5) và (6) \(\Rightarrow MQ//PN,MQ=PN\)
Xét tứ giác MQPN có \(\Rightarrow MQ//PN,MQ=PN\)
\(\Rightarrow MQPN\)là hình bình hành (dhnb)
\(\Rightarrow MP\)giao QN tại trung điểm mỗi đường (tc) (7)
Từ (4) và (7) \(\Rightarrow MP,NQ,EF\)cắt nhau tại một điểm
c) Xét tam giác ABD có Q là trung điểm của AD (gt), F là trung điểm của BD(gt)
\(\Rightarrow QF\)là đường trung bình của tam giác ADB
\(\Rightarrow QF//AB\left(8\right)\)
CMTT: \(FN//CD\)và \(EN//AB\)
Mà Q,F,E,N thẳng hàng
\(\Rightarrow AB//CD\)
Vậy để Q,F,E,N thẳng hàng thì tứ giác ABCD phải thêm điều kiện \(AB//CD\)
Tối về mình làm nốt nhé giờ mình có việc
Bài 4 :
Để tứ giác ABCD là hình bình hành
\(\Leftrightarrow\hept{\begin{cases}\widehat{DAB}=\widehat{DCB}=120^o\\\widehat{ADC}=\widehat{ABC}\end{cases}}\)
Lại có : \(\widehat{DAB}+\widehat{DCB}+\widehat{ABC}+\widehat{ADC}=360^o\)
\(\Leftrightarrow\widehat{ABC}+\widehat{ADC}=120^o\)
\(\Leftrightarrow\widehat{ABC}=\widehat{ADC}=60^o\)
Xem thêm câu trả lời
Cho tam giác ABC cân tại A Gọi M N lần lượt là trung điểm AB AC BC
A)chứng minh tứ giác BMC là hình thang cân
B)Gọi K là điểm đối xứng với h qua n Chứng minh a h c k là hình chữ nhậtt
C) Chứng minh tứ giác M N là hình thoi
D) Kẻ AE vuông góc AC Gọi I là trung điểm AC Chứng minh AE vuông với BE
Bài 4.Cho tam giác ABC cân tại A.Gọi D, E, H lần lượt là trung điểm của AB, AC và BC.
a) Tứ giác ADHE là hình gì?
b) Trên tia HE lấy điểm M sao cho HE = EM.Tứ giác AHCM là hình gì?
c) Gọi I là điểm đối xứng của H qua D. Chứng minh A là trung điểm của IM.
d) Tìm điều kiện của tam giác ABC để tứ giác ADHM là hình thang cân.
a: Xét tứ giác ADHE có
HD//AE
HD=AE
Do đó: ADHE là hình bình hành
mà AD=AE
nên ADHE là hình thoi
Đúng 1
Bình luận (0)
Cho ∆ABC nhọn (AB < AC). Gọi D; E và F lần lượt là trung điểm AB; AC và BC.
a) Chứng minh DEFB là hình bình hành.
b) Chứng minh ADFE là hình bình hành.
c) Chứng minh DECF là hình bình hành.
d) Gọi I là trung điểm DE. Chứng minh A; I và F thẳng hàng.














![[Shima nightcore]](https://hoc24.vn/images/avt/avt1557774_256by256.jpg)

