Giới hạn l i m x → 0 x + 9 + x + 16 - 7 x bằng a b (phân số tối giản) thì giá trị A = b a - b 8 là:
A. 7 24
B. 3 7
C. 22 7
D. 7 22
Những câu hỏi liên quan
Cho hàm số y=f(x) =1/√(2-x). Khẳng định nào sau đây đúng:
A. Hàm số chỉ có giới hạn tại điểm x=2
B. Hàm số có giới hạn trái và giới hạn phải bằng nhau
C. Hàm số có giới hạn tại điểm x=2
D. Hàm số chỉ có giới hạn trái tại điểm x=2
Do \(x< 2\) nên x chỉ tiến tới 2 từ phía trái
Do đó hàm số chỉ có giới hạn trái tại điểm x=2 (giới hạn bằng dương vô cực)
Đúng 0
Bình luận (0)
Cho hàm số \(f\left(x\right)=x^2-2x+3\) . Khẳng định nào sau đây là sai:
A, Hàm số có giới hạn trái và phải tại điểm x=1 bằng nhau
B, Hàm số có giới hạn trái và phải tại mọi điểm bằng nhau
C, Hàm số có giới hạn tại mọi điểm
D, Cả ba khẳng định trên là sai
Đáp án D sai
Hàm đa thức có giới hạn tại mọi điểm và tại tất cả các điểm thì giới hạn trái luôn bằng giới hạn phải
Bài 1: Giới hạn của dãy số sau đây bằng bao nhiêu:
A. 3 B. C. 0 D.
Bài 2: Giới hạn của dãy số sau đây bằng bao nhiêu:
A. 1 B. C. 0 D.
Bài 3: Giới hạn của dãy số sau đây bằng bao nhiêu:
A. 7 B. C. 0 D.
Bài 4: Giới hạn của dãy số sau đây bằng bao nhiêu:
A. B. 2 C. 0 D.
Bài 5: Giới hạn của dãy số sau đây bằng bao nhiêu:
A. 0 B. 1 C. D.
Bài 6: Giới hạn của hàm số sau đây bằng bao nhiêu:
A. B. 2 C. D. 8
Bài 7: Giới hạn của hàm số sau đây bằng bao nhiêu:
A. B. 2 C. 0 D.
Bài...
Đọc tiếp
Bài 1: Giới hạn của dãy số sau đây bằng bao nhiêu:
A. 3 B. C. 0 D.
Bài 2: Giới hạn của dãy số sau đây bằng bao nhiêu:
A. 1 B. C. 0 D.
Bài 3: Giới hạn của dãy số sau đây bằng bao nhiêu:
A. 7 B. C. 0 D.
Bài 4: Giới hạn của dãy số sau đây bằng bao nhiêu:
A. B. 2 C. 0 D.
Bài 5: Giới hạn của dãy số sau đây bằng bao nhiêu:
A. 0 B. 1 C. D.
Bài 6: Giới hạn của hàm số sau đây bằng bao nhiêu:
A. B. 2 C. D. 8
Bài 7: Giới hạn của hàm số sau đây bằng bao nhiêu:
A. B. 2 C. 0 D.
Bài 8: Giới hạn của hàm số sau đây bằng bao nhiêu:
A. 2 B. 3 C. 4 D. 5
Bài 9: Giới hạn của hàm số sau đây bằng bao nhiêu:
A. 0 B. 1 C. D. 2
Bài 10: Giới hạn của hàm số sau đây khi x tiến đến 0 : bằng bao nhiêu
A. 0 B. 1 C. D.
Cho a, b là 2 số dương thỏa mãn giới hạn \(I=\lim\limits_{x\rightarrow+\infty}\left(ax-\sqrt{bx^2-2x+2018}\right)\) hữu hạn. Tính I
\(\lim\limits_{x\rightarrow+\infty}\left(ax-\sqrt{bx^2-2x+2018}\right)=\lim\limits_{x\rightarrow+\infty}x.\lim\limits_{x\rightarrow+\infty}\left(a-\sqrt{b}\right)=\pm\infty\)
Còn tuỳ vào độ lớn của a và b
nếu lim f(x)=L>0, lim g(x)=-vô cùng thì kết quả của giới hạn lim f(x).g(x) là:
A/ - vô cùng
B/ 0
C/ + vô cùng
D/ L
Xem thêm câu trả lời
Câu này làm như nào vậy ạ?
Đề bài: Tìm diện tích của hình phẳng giới hạn bởi hai đường cong có phương trình \(x-y^2=0\) và \(x+2y^2-12=0\).
Pt tọa độ giao điểm:
\(\left\{{}\begin{matrix}x-y^2=0\\x+2y^2-12=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y^2=x\\x+2x-12=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=4\\y=\pm2\end{matrix}\right.\)
Cũng từ 2 pt ta được \(\left\{{}\begin{matrix}x=y^2\\x=12-2y^2\end{matrix}\right.\)
Trên đoạn \(\left[-2;2\right]\), ta thấy \(12-2y^2\ge y^2\)
Vậy diện tích hình phẳng cần tìm:
\(S=\int\limits^2_{-2}\left(12-2y^2-y^2\right)dy=\left(12y-y^3\right)|^2_{-2}=32\) (đvdt)
Đúng 0
Bình luận (1)
Tìm m để các hàm số
f
(
x
)
x
2
+
m
x
+
2
m
+
1
x
+...
Đọc tiếp
Tìm m để các hàm số f ( x ) = x 2 + m x + 2 m + 1 x + 1 k h i x ≥ 0 2 x + 3 m - 1 1 - x + 2 k h i x < 0 có giới hạn khi x → 0.
A. 1 3
B. - 1 3
C. - 2 3
D. - 4 3
- Ta có:
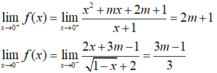
- Hàm số có giới hạn khi x → 0 khi và chỉ khi:
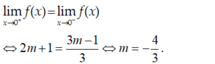
Chọn D.
Đúng 0
Bình luận (0)
Giới hạn
lim
x
→
2
+
x
2
-
2
x
2
-
x
bằng -
m
, m
0. Giá trị biểu thức A m2 - 2m là: A . - 1 B . - 2 C .8 D . 1
Đọc tiếp
Giới hạn lim x → 2 + x 2 - 2 x 2 - x bằng - m , m 0. Giá trị
biểu thức A = m2 - 2m là:
A . - 1
B . - 2
C .8
D . 1
Cho hàm số
f
x
x
+
4
−
2
x
khi
x
0
m...
Đọc tiếp
Cho hàm số f x = x + 4 − 2 x khi x > 0 m x + m + 1 4 khi x ≤ 0 , m là tham số. Tìm giá trị của m để hàm số có giới hạn tại x = 0
A. m = 1 2
B. m = 1
C. m = 0
D. m = − 1 2
Cho hàm số
f
x
x
+
4
-
2
x
,
x
0...
Đọc tiếp
Cho hàm số f x = x + 4 - 2 x , x > 0 m x + m + 1 4 , x ≤ 0 , m là tham số. Tìm giá trị của tham số m để hàm số có giới hạn tại x = 0.
A. m = 1
B. m = 0
C. m = 1 2
D. m = - 1 2
Đáp án B
Ta có lim x → 0 + x + 4 - 2 x = lim x → 0 + x + 4 - 2 x + 4 - 2 2 = lim x → 0 + 1 x + 4 + 2 = 1 4
Và lim x → 0 - f x = lim x → 0 - m x + m + 1 4 = m + 1 4
Yêu cầu bài toán lim x → 0 + f ( x ) = lim x → 0 - f ( x ) ⇔ m = 0 .
Đúng 0
Bình luận (0)