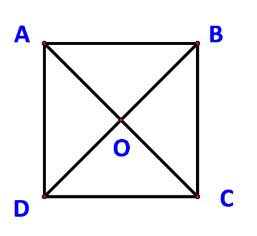
a) Do ABCD cũng là một hình bình hành nên \(\overrightarrow {DA}  + \overrightarrow {DC}  = \overrightarrow {DB} \)

\( \Rightarrow \;|\overrightarrow {DA}  + \overrightarrow {DC} |\; = \;|\overrightarrow {DB} |\; = DB = a\sqrt 2 \)

b) Ta có: \(\overrightarrow {AD}  + \overrightarrow {DB}  = \overrightarrow {AB} \) \( \Rightarrow \overrightarrow {AB}  - \overrightarrow {AD}  = \overrightarrow {DB} \)

\( \Rightarrow \left| {\overrightarrow {AB}  - \overrightarrow {AD} } \right| = \left| {\overrightarrow {DB} } \right| = DB = a\sqrt 2 \)

c) Ta có: \(\overrightarrow {DO}  = \overrightarrow {OB} \)

\( \Rightarrow \overrightarrow {OA}  + \overrightarrow {OB}  = \overrightarrow {OA}  + \overrightarrow {DO}  = \overrightarrow {DO}  + \overrightarrow {OA}  = \overrightarrow {DA} \)

\( \Rightarrow \left| {\overrightarrow {OA}  + \overrightarrow {OB} } \right| = \left| {\overrightarrow {DA} } \right| = DA = a.\)

a: AB=BC=CD=DA=6a

\(AC=BD=\sqrt{\left(6a\right)^2+\left(6a\right)^2}=6a\sqrt{2}\)

\(\left|\overrightarrow{AB}-\overrightarrow{AC}\right|=\left|\overrightarrow{CA}+\overrightarrow{AB}\right|=CB=6a\)

\(\left|\overrightarrow{BC}+\overrightarrow{BD}\right|=\sqrt{BC^2+BD^2+2\cdot BC\cdot BD\cdot cos45}\)

\(=\sqrt{36a^2+72a^2+\sqrt{2}\cdot6a\cdot6a\sqrt{2}}\)

\(=6a\sqrt{5}\)

b: \(\overrightarrow{AB}\cdot\overrightarrow{AC}=AB\cdot AC\cdot cos\left(\overrightarrow{AB},\overrightarrow{AC}\right)=6a\cdot6a\sqrt{2}\cdot\dfrac{\sqrt{2}}{2}\)

\(=36a^2\)

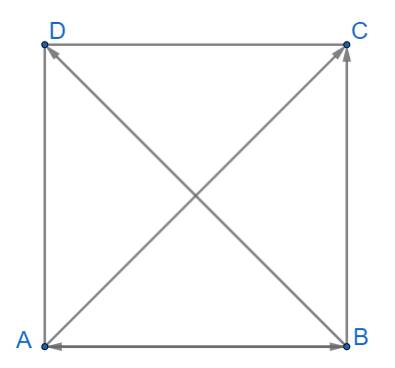
Ta có: \(AC = BD = \sqrt {A{B^2} + B{C^2}}  = \sqrt {{a^2} + {a^2}}  = a\sqrt 2 \)

+) \(AB \bot AD \Rightarrow \overrightarrow {AB}  \bot \overrightarrow {AD}  \Rightarrow \overrightarrow {AB} .\overrightarrow {AD}  = 0\)

+) \(\overrightarrow {AB} .\overrightarrow {AC}  = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = a.a\sqrt 2.\cos 45^\circ  = a^2\)

+) \(\overrightarrow {AC} .\overrightarrow {CB}  = \left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {CB} } \right|.\cos \left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right) = a\sqrt 2 .a.\cos 135^\circ  =  - {a^2}\)

+) \(AC \bot BD \Rightarrow \overrightarrow {AC}  \bot \overrightarrow {BD}  \Rightarrow \overrightarrow {AC} .\overrightarrow {BD}  = 0\)

Chú ý

\(\overrightarrow {a}  \bot \overrightarrow {b}  \Leftrightarrow \overrightarrow {a} .\overrightarrow {b}  = 0\)

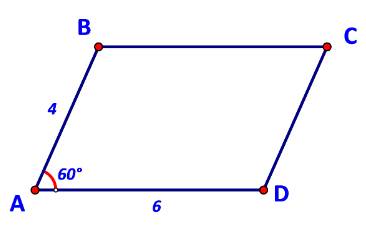
a) \(\overrightarrow {BD}  = \overrightarrow {AD}  - \overrightarrow {AB} ;\;\overrightarrow {AC}  = \overrightarrow {AB}  + \overrightarrow {AD} .\)

b) \(\overrightarrow {AB} .\overrightarrow {AD}  = 4.6.\cos \widehat {BAD} = 24.\cos {60^o} = 12.\)

\(\begin{array}{l}\overrightarrow {AB} .\overrightarrow {AC}  = \overrightarrow {AB} (\overrightarrow {AB}  + \overrightarrow {AD} ) = {\overrightarrow {AB} ^2} + \overrightarrow {AB} .\overrightarrow {AD}  = {4^2} + 12 = 28.\\\overrightarrow {BD} .\overrightarrow {AC}  = (\overrightarrow {AD}  - \overrightarrow {AB} )(\overrightarrow {AB}  + \overrightarrow {AD} ) = {\overrightarrow {AD} ^2} - {\overrightarrow {AB} ^2} = {6^2} - {4^2} = 20.\end{array}\)

c) Áp dụng định lí cosin cho tam giác ABD ta có:

\(\begin{array}{l}\quad \;B{D^2} = A{B^2} + A{D^2} - 2.AB.AD.\cos A\\ \Leftrightarrow B{D^2} = {4^2} + {6^2} - 2.4.6.\cos {60^o} = 28\\ \Leftrightarrow BD = 2\sqrt 7 .\end{array}\)

Áp dụng định lí cosin cho tam giác ABC ta có:

\(\begin{array}{l}\quad \;A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\\ \Leftrightarrow A{C^2} = {4^2} + {6^2} - 2.4.6.\cos {120^o} = 76\\ \Leftrightarrow AC = 2\sqrt {19} .\end{array}\)

a)       \(\begin{array}{l}\overrightarrow a  = \left( {\overrightarrow {AC}  + \overrightarrow {BD} } \right) + \overrightarrow {CB}  = \left( {\overrightarrow {AC}  + \overrightarrow {CB} } \right) + \overrightarrow {BD} \\ = \overrightarrow {AB}  + \overrightarrow {BD}  = \overrightarrow {AD}\\  \Rightarrow |{\overrightarrow a}|= \left| {\overrightarrow {AD} } \right| = AD = 1\end{array}\)

b)       \(\begin{array}{l}\overrightarrow a  = \overrightarrow {AB}  + \overrightarrow {AD}  + \overrightarrow {BC}  + \overrightarrow {DA}  = \left( {\overrightarrow {AB}  + \overrightarrow {BC} } \right) + \left( {\overrightarrow {AD}  + \overrightarrow {DA} } \right)\\ = \overrightarrow {AC}  + \overrightarrow {AA}  = \overrightarrow {AC}  + \overrightarrow 0  = \overrightarrow {AC} \end{array}\)

\(AC = \sqrt {A{B^2} + B{C^2}}  = \sqrt {{1^2} + {1^2}}  = \sqrt 2 \)

\(\Rightarrow |{\overrightarrow a}|= \left| {\overrightarrow {AC} } \right| = \sqrt 2 \)