Cho hình lăng trụ lục giác đều ABCDEF. A’B’C’D’E’F’ có cạnh đáy bằng a, chiều cao h.
a/ Tính diện tích xung quanh và thể thể tích hình trụ ngoại tiếp hình lăng trụ.
b/ Tính diện tích toàn phần và thể tích hình trụ nội tiếp hình lăng trụ.
Lời giải:
a)
- Diện tích xung quanh :\(S_{xq}=6ah\)
Xét hình lục giác đều \(ABCDEF\), ta thấy đường kính hình tròn ngoại tiếp hình lục giác trên chính là đoạn \(AD=BE=CF\)
Kẻ \(FH\perp AD\). Dễ thấy \(\angle FAB=120^0\Rightarrow \angle FAD=\angle FAH=60^0\)
\(\Rightarrow AH=\cos 60.a=\frac{a}{2}\)
\(\Rightarrow AD=FE+2AH=2a\Rightarrow 2R=2a\rightarrow R=a\)
Thể tích hình trụ: \(V=\pi R^2h=\pi a^2h\)
b)
Diện tích toàn phần: \(S_{tp}=S_{xq}+2S_{ABCDEF}\)
Từ phần a ta cũng suy ra \(FH=\frac{\sqrt{3}a}{2}\)
Xét hình thang \(AFED\): \(S_{AFED}=\frac{(EF+AD).FH}{2}=\frac{3\sqrt{3}a^2}{4}\)
\(\Rightarrow S_{ABCDEF}=\frac{3\sqrt{3}a^2}{2}\)
Do đó \(S_{tp}=6ha+3\sqrt{3}a^2\)
Ta thấy: Đường kính đường tròn nội tiếp hình lục giác đều chính là khoảng cách từ \(BC\rightarrow FE\) hay \(2r=FB\)
Xét tam giác \(FAB\) , sử dụng định lý hàm cos ta thu được \(2r=FB=\sqrt{3}a\)\(\Rightarrow r=\frac{\sqrt{3}a}{2}\)
Do đó thể tích là: \(V=\pi r^2h=\frac{3\pi a^2h}{4}\)
Cho hình lăng trụ ngũ giác ABCD.A'B'C'D'. Gọi A'', B'', C'', D'', E'' lần lượt là trung điểm của các cạnh AA', BB', CC', DD', EE'. Tỉ số thể tích giữa khối lăng trụ ABCDE.A''B''C''D''E'' và khối lăng trụ ABCDE.A'B'C'D' bằng:
A. 1/2 B. 1/4
C. 1/8 D. 1/10.
Chọn A.
Để ý rằng hai khối lăng trụ đó có diện tích đáy bằng nhau, tỉ số hai đường cao tương ứng bằng 1/2.
a.1/2
okkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkk
Cho lục giác đều $A B C D E F$ tâm $O$. Chứng minh: $\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}+\overrightarrow{O D}+\overrightarrow{O E}+\overrightarrow{O F}=\overrightarrow{0}$.
Tính diện tích xung quanh , diện tích toàn phần và thể tích của lăng trụ đứng có chiều cao h và cạnh đáy lần lượt là: a)hình vuông cạnh a b)Tam giác đều cạnh a c) lục giác đều cạnh a d) hình thang cân,đáy lớn là 2a,các cạnh còn lại a e) hình thoi có 2 đường chéo là 6a và 8a
Tính diện tích xung quanh, diện tích toàn phần và thể tích của lăng trụ đứng có chiều cao h và đáy lần lượt là:
a) Hình vuông cạnh a;
b) Tam giác đều cạnh a;
c) Lục giác đều cạnh a;
d) Hình thang cân, đáy lớn là 2a, các cạnh còn lại bằng a;
e) Hình thoi có hai đường chéo là 6a và 8a.
Gọi h là chiều cao của hình lăng trụ đứng.
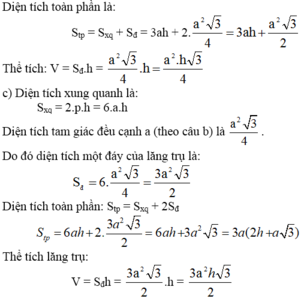
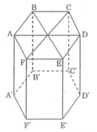
Cho lục giác đều ABCDEF . A' ; B' ; C' ; D' ; E' ; F' , là trung điểm AB , CD , DE , EF , FA
Chứng minh A'B'C'D'E'F' là lục giác đều
Giải chi tiết giùm nha
Theo đường tb tam giác
A'B'=1/2AC
B'C'=1/2BD
C'D'=1/2CE
D'E'=1/2DF
E'F'=1/2AE
A'F'=1/2BF
Mà AC=BD=CE=DF=AE=BF(tính chất lục giác)
=>A'B'C'D'E'F' là lục giác đều
Bài 3: Cho lục giác ABCDEF có số đo các góc (tính theo độ) là 1 số nguyên và góc A-góc B=góc B-góc C=góc C-góc D=góc D-góc E=góc E-góc F. Tính giá trị lớn nhất của góc A.
Bài 4: Cho lục giác đều ABCDEF. M, N lần lượt là trung điểm của CD, DE. AM cắt BN tại I.
a) Góc AIB=?
b) Góc OID=? (biết O là tâm của lục giác đều)
Một lăng trụ đứng lục giác đều có độ dài cạnh đáy là 6cm, chiều cao của lăng trụ là 10cm. Diện tích toàn phần của lăng trụ đó là (đơn vị c m 2 )
A.180 -54 3
B.180 + 108 3
C.360 - 54 3
D.360 + 108 3
Hãy chọn kết quả đúng
Nối các đường chéo AD,BE,CF của mặt đáy .Các đường chéo chia lục giác ra thành 6 tam giác đều bằng nhau có cạnh là 6 (cm)
Diện tích mặt đáy bằng diện tích một tam giác đều cạnh 6cm nhân với 6
Cho lục giác đều ABCDEF tâm O. Số các vecto khác vecto - không, có điểm đầu cuối lấy từ 7 điểm A, B, C, D, E, F, O là
Số vecto khác vecto 0, có điểm đầu điểm cuối lấy từ 7 điểm A,B,C,D,E,F,O là:
\(A^2_7=7\cdot6=42\left(vecto\right)\)
đúng ko v ???????
