Chọn A.
Để ý rằng hai khối lăng trụ đó có diện tích đáy bằng nhau, tỉ số hai đường cao tương ứng bằng 1/2.
a.1/2
okkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkk
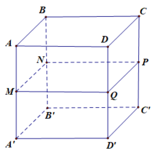
Cho hình hộp ABCD.A'B'C'D' có AB = AD = 2a, AA' = 4a . Lấy M, N, P, Q lần lượt là trung điểm của AA’, BB’, CC’, DD’. Biết hình hộp chữ nhật ABCD.A'B'C'D' nội tiếp khối trụ (T) và lăng trụ ABCD.MNPQ nội tiếp mặt cầu (C). Tỉ số thể tích V T V C giữa khối cầu và khối trụ là.
Cho hình hộp A B C D . A ' B ' C ' D ' có A B = A D = 2 a , A A ' = 4 a Lấy M, N, P, Q lần lượt là trung điểm của A A ' , B B ' , C C ' , D D ' Biết hình hộp chữ nhật A B C D . A ' B ' C ' D ' nội tiếp khối trụ (T) và lăng trụ A B C D . M N P Q nội tiếp mặt cầu (C) Tỉ số thể tích V ( T ) V ( C ) giữa khối trụ và khối cầu là:
A. 2 3 3
B. 3 3
C. 2 3 3
D. 1 3 2
Cho hình hộp A B C D . A ' B ' C ' D ' có A B = A D = 2 a , A A ' = 4 a . Lấy M, N, P, Q lần lượt là trung điểm của AA’, BB’,CC, DD’. Biết hình hộp chữ nhật A B C D . A ' B ' C ' D ' nội tiếp khối trụ (T) và lăng trụ ABCD.MNPQ nội tiếp mặt cầu (C). Tỉ số thể tích V ( T ) V ( C ) giữa khối cầu và khối trụ là
A. 2 3 3
B. 3 3
C. 2 3 3
D. 1 3 2
Cho hình hộp ABCD.A'B'C'D' có AB = AD = 2a,AA' = 4a. Lấy M, N, P, Q lần lượt là trung điểm của . Biết hình hộp chữ nhật AA', BB', CC' Đ' nội tiếp khối trụ (T) và lăng trụ ABCD.MNPQ nội tiếp mặt cầu (C). Tỉ số thể tích V T V C giữa khối cầu và khối trụ
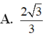
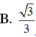
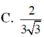
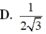
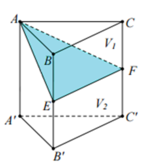
Cho hình lăng trụ ABC.A'B'C'. Gọi E, F lần lượt là trung điểm của BB¢ và CC¢. Mặt phẳng (AEF) chia khối lăng trụ thành hai phần có thể tích V 1 và V 2 như hình vẽ. Tỉ số V 1 V 2 là
A. 1 2
B. 1
C. 1 3
D. 1 4
Cho hình lăng trụ ABC.A’B’C’. Gọi E, F lần lượt là trung điểm của BB’ và CC’. Mặt phẳng (AEF) chia khối lăng trụ thành 2 phần có thể tích V1 và V2 như hình vẽ. Khi đó tỉ số V 1 V 2 có giá trị là
A. 1 4
B. 1 2
C. 1 3
D. 3 4
Cho hình lăng trụ ABC.A’B’C’. Gọi E, F lần lượt là trung điểm của BB’ và CC’. Mặt phẳng (AEF) chia khối lăng trụ thành 2 phần có thể tích V1 và V2 như hình vẽ. Khi đó tỉ số V 1 V 2 có giá trị là
A. 1 4
B. 1 2
C. 3
D. 1 3
Cho khối lăng trụ tam giác ABC. A'B'C'. Gọi M, N lần lượt là trung điểm của BB' và CC'. Mặt phẳng (AMN) chia khối lăng trụ thành hai phần. Gọi V₁ là thể tích của khối đa diện chứa đỉnh B' và V₂ là thể tích khối đa diện còn lại. Tính tỉ số V₁/V₂.
A. V 1 V 2 = 7 2
B. V 1 V 2 = 2
C. V 1 V 2 = 1 3
D. V 1 V 2 = 5 2
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N lần lượt là trung điểm của BB’, CC’. Mặt phẳng (A’MN) chia khối lăng trụ thành hai phần, V 1 là thể tích của phần đa diện chứa điểm B, V 2 thể tích phần đa diện còn lại. Tính tỉ số V 1 V 2
A. V 1 V 2 = 7 2
B. V 1 V 2 = 2
C. V 1 V 2 = 3
D. V 1 V 2 = 5 2
