Tìm tất cả các giá trị thực của x để đồ thị hàm số y = log 0 , 5 x nằm phía trên đường thẳng y=2
A. x ≥ 1 4
B. 0 < x ≤ 1 4
C. 0 < x < 1 4
D. x ≥ 1 4
Tìm tất cả các giá trị thực của x để đồ thị hàm số y = log0,5x nằm phía trên đường thẳng y = 2
![]()
![]()
Đáp án C
Ta có log0,5x > 2 <=> 0 < x < 1 4
Tìm tất cả các giá trị thực của x để đồ thị hàm số y = l o g 0 , 5 x nằm phía trên đường thẳng y = 2
A. x ≥ 1 4
B. 0 < x ≤ 1 4
C. 0 < x < 1 4
D. x > 1 4
Đáp án C
Ta có log 0 , 5 x > 2 ⇔ 0 < x < 1 4 .
Cho đồ thị của hàm số \(y = {\log _2}x\) và y = 2 như Hình 6.8. Tìm khoảng giá trị của x mà đồ thị hàm số \(y = {\log _2}x\) nằm phía trên đường thẳng y = 2 và từ đó suy ra tập nghiệm của bất phương trình \({\log _2}x > 2.\)

Khoảng giá trị của x mà đồ thị hàm số \(y=log_2x\) nằm phía trên đường thẳng y = 2 là \(\left(4;+\infty\right)\)
\(\Rightarrow\) Tập nghiệm của bất phương trình \(log_2x>2\) là \(\left(4;+\infty\right)\)
Tìm tất cả giá trị thực của m để đồ thị hàm số y = 1 3 x 3 - m x 2 + ( 2 m + 1 ) x - 3 có hai cực trị nằm cùng phía với trục tung.
A. m ∈ ( 1 ; + ∞ )
B. m ∈ 1 2 ; 1 ∪ ( 1 ; + ∞ )
C. m ∈ 1 2 ; + ∞
D. m ∈ - ∞ ; 1 2
Tìm tất cả các giá trị thực của tham số m để hàm số y = x^3 - (3m +1).x^2 + (2m -1)x +m +1 . Có bao nhiêu số tự nhiên m<100 để đồ thị hs có hai điểm cực trị nằm về 2 phía của trục hoành.
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = 1 3 x 3 − m − 1 x 2 + m − 1 x + m 2 có hai điểm cực trị nằm về phía bên phải trục tung.
A. m < 0
B. m < 1
C. m > 2
D. m > 0
Đáp án C
TXĐ: D = ℝ .
Ta có y ' = x 2 − 2 m − 1 x + m − 1 .
Để đồ thị hàm số có hai điểm cực trị nằm về hai phía của trục tung thì
m − 1 2 − m − 1 > 0 m − 1 > 0 2 m − 1 > 0 ⇔ m > 2.
Vậy m>2 thỏa mãn điều kiện đề bài.
Cho hàm số y=f(x) có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = f x + m có 5 điểm cực trị.
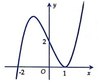
A. m ≤ − 1
B. m < − 1
C. m ≥ − 1
D. m > − 1
Cho hàm số y=f(x) có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = f x + m có 5 điểm cực trị.
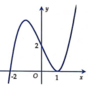
A. m ≤ − 1
B. m < − 1
C. m ≥ − 1
D. m > 1
Đáp án B.
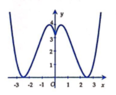
Hàm số y = f x + m là một hàm số chẵn nên đồ thị đối xứng qua trục Oy. Mặt khác y = f x + m = f x + m ∀ x ≥ 0 . Ta có phép biến đổi từ đồ thị hàm số y = f x thành đồ thị hàm số y = f x + m :
* Nếu m > 0:
- Bước 1: Tịnh tiến đồ thị hàm số y = f x sang trái m đơn vị.
- Bước 2: Xóa phần nằm bên trái Oy của đồ thị thu được ở Bước 1.
- Bước 3: Lấy đối xứng đồ thị thu được ở Bước 2 qua Oy.
* Nếu m=0 :
- Bước 1: Tịnh tiến đồ thị hàm số y = f x sang phải m đơn vị.
- Bước 2: Xóa phần nằm bên trái Oy của đồ thị thu được ở Bước 1.
- Bước 3: Lấy đối xứng đồ thị thu được ở Bước 2 qua Oy.
Quan sát ta thấy đồ thị hàm số y = f x có 2 điểm cực trị.
Để đồ thị hàm số y = x + m có 5 điểm cực trị thì nhánh bên phải Oy của đồ thị hàm số y = x + m phải có 2 điểm cực trị => Điểm cực trị của đồ thị hàm số y = f x phải được tịnh tiến sang phải O y ⇒ m < − 1 .
Cho hàm số y=f(x)(x-1) xác định và liên tục trên R và có đồ thị như hình vẽ dưới đây. Tìm tất cả các giá trị thực của tham số m để đường thẳng y = m 2 - m cắt đồ thị hàm số f x x - 1 tại 2 điểm có hoành độ nằm ngoài đoạn [-1;1]
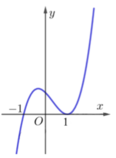
A. m > 0
B. [ m > 1 m < 0
C. m < 1
D. 0 < m < 1
Đáp án B
Lấy đối xứng đồ thị hàm số f(x)(x-1) qua trục Ox ta được đồ thị của hàm số f x x - 1 . Từ đồ thị hàm số f x x - 1 ta thấy đường thẳng y = m 2 - m cắt hàm số f x x - 1 tại 2 điểm nằm ngoài [-1;1]
⇔ m 2 - m > 0 ⇔ [ m < 0 m > 1