Tìm tất cả các giá trị của m để hệ phương trình x + y = 2 x 2 y + x y 2 = 4 m 2 - 2 m có nghiệm
A. 0 ; 1 2
B. - 1 ; 1 2
C. [ 1 ; + ∞ )
D. - 1 2 ; 1
cho hê phương trình\(\left\{{}\begin{matrix}x+y=m+1\\x^2+y^2+xy=m^2+2\end{matrix}\right.\)tìm tất cả các giá trị của m để hệ phương trình có nghiệm
tìm tất cả các giá trị của m để hệ phương trình {2x+3y=4 (m+2)x+(m+1)y=3 vô nghiệm
Để hệ vô nghiệm thì 2/m+2=3/m+1<>4/3
=>3m+6=2m+2 và 3/m+1<>4/3
=>m=-4 và 3/-3<>4/3(luôn đúng)
=>m=-4
`{(2x+3y=4),((m+2)x+(m+1)y=3):}` vô nghiệm
`<=>[m+2]/2=[m+1]/3 ne 3/4`
`<=>{(3m+6=2m+2),(4m+8 ne 6),(4m+4 ne 9):}`
`<=>{(m=-4),(m ne -1/2),(m ne 5/4):}`
`<=>m=-4`
Cho hệ phương trình\(\left\{{}\begin{matrix}ax-y=2\\x+ay=3\end{matrix}\right.\) . Tìm tất cả các giá trị của tham số m để hệ phương trình duy nhất.
Tìm tất cả các giá trị của tham số m để hệ phương trình x 2 - m = y ( x + m y ) x 2 - y = x y có nghiệm
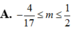
![]()
![]()
![]()
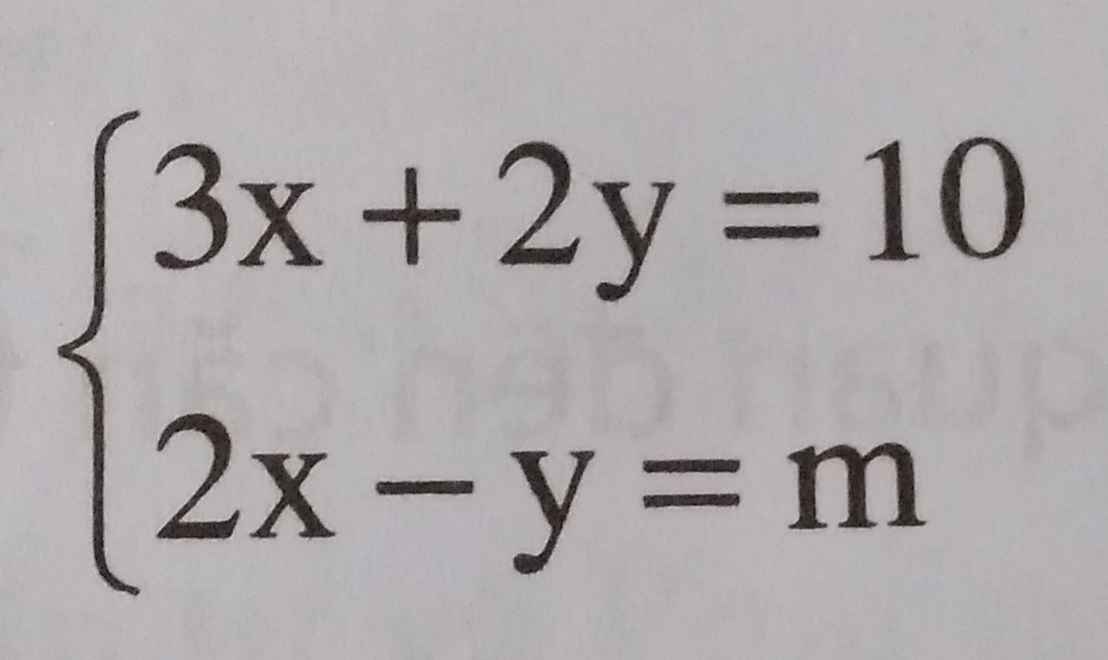
tìm tất cả các giá trị thực của tham số m để hệ phương trình có nghiệm (x;y) thỏa x>0, y<0.
\(\left\{{}\begin{matrix}3x+2y=10\\y=2x-m\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}3x+2(2x-m)=10\\y=2x-m\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}3x+4x-2m=10\\y=2x-m\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}7x=10+2m\\y=2x-m\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}x=\dfrac{2m+10}{7}\\y=\dfrac{4m+20}{7}-m\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}x=\dfrac{2m-10}{7}\\y=\dfrac{20-3m}{7}\end{matrix}\right.\)
Thay x và y vừa tìm dc vào điều kiện X>0 và Y<0
\(\dfrac{2m-10}{7}\)>0 => 2m-10>0 <=> m>5
\(\dfrac{20-3m}{7}\)<0 => 20-3m>0 <=> m<20/3
Vậy ...
Bài 3: Cho hệ phương trình:
\(\left\{{}\begin{matrix}mx-y=1\\2x+my=4\end{matrix}\right.\)
a) Giải hệ khi m=1
b) Tìm tất cả các giá trị của m để hệ phương trình có nghiệm duy nhất (x;y) thỏa mãn x+y=2
a: Thay m=1 vào hệ phương trình, ta được:
\(\left\{{}\begin{matrix}x-y=1\\2x+y=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x=5\\x-y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{3}\\y=x-1=\dfrac{5}{3}-1=\dfrac{2}{3}\end{matrix}\right.\)
b: Để hệ có nghiệm duy nhất thì \(\dfrac{m}{2}\ne-\dfrac{1}{m}\)
=>\(m^2\ne-2\)(luôn đúng)
\(\left\{{}\begin{matrix}mx-y=1\\2x+my=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=mx-1\\2x+m\left(mx-1\right)=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=mx-1\\x\left(m^2+2\right)=m+4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{m+4}{m^2+2}\\y=\dfrac{m\left(m+4\right)}{m^2+2}-1=\dfrac{m^2+4m-m^2-2}{m^2+2}=\dfrac{4m-2}{m^2+2}\end{matrix}\right.\)
x+y=2
=>\(\dfrac{m+4+4m-2}{m^2+2}=2\)
=>\(2m^2+4=5m+2\)
=>\(2m^2-5m+2=0\)
=>(2m-1)(m-2)=0
=>\(\left[{}\begin{matrix}2m-1=0\\m-2=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}m=\dfrac{1}{2}\\m=2\end{matrix}\right.\)
Tìm tất cả các giá trị thực của tham số m để hệ phương trình sau có nghiệm x 2 + 4 x + y = m 2 x 2 + x y ( x + 2 ) = 9
A. m ≥ 6
B. - 10 ≤ m ≤ 6
C. m ≤ - 10
D. m ≤ - 10 hoặc m ≥ 6
Cho hệ phương trình \(\left\{{}\begin{matrix}x+y=2\\x^2y+xy^2=4m^2-2m\end{matrix}\right.\)
Tìm tất cả các giá trị của m để hệ trên có nghiệm.
- Từ PT ( II ) ta có : \(xy\left(x+y\right)=2xy=4m^2-2m\)
\(\Rightarrow xy=2m^2-m\)
- Hệ PT trên có nghiệm là nghiệm của PT :
\(x^2-2x+2m^2-m=0\) ( I )
Có : \(\Delta^,=b^{,2}-ac=1-\left(2m^2-m\right)=-2m^2+m-1\)
- Để PT ( i ) có nghiệm \(\Leftrightarrow\Delta^,>0\)
\(\Leftrightarrow-2m^2+m-1>0\)
Vậy không tồn tại m để hệ phương trình có nghiệm .
Cho hệ phương trình \(\left\{{}\begin{matrix}\left(m-1\right)x+y=2\\x+2y=2\end{matrix}\right.\) ( m là tham số và x,y là các ẩn số)
Tìm tất cả các giá trị nguyên của m để hệ phương trình có nghiệm (x,y) trong đó x,y là các số nguyên
Giải
Từ phương trình thứ hai ta có: x= 2 - 2y thế vào phương trình thứ nhất được:
(m-1)(2-2y) + y =2
<=> ( 2m - 3)y= 2m-4 (3)
Hệ có nghiệm x,y là các số nguyên <=> (3) có nghiệm y nguyên.
Với m thuộc Φ => 2m-3 khác 0 => (3) có nghiệm y=\(\dfrac{2m-4}{2m-3}\)
y thuộc Φ <=> \(\left[{}\begin{matrix}2m-3=1\\2m-3=-1\end{matrix}\right.< =>\left[{}\begin{matrix}m=2\\m=1\end{matrix}\right.\)
Vậy có hai giá trị m thỏa mãn:1,2.