Cho tam giác ABC có ba góc nhọn. Vẽ các đường cao AI, BK, CL của tam giác ấy. Gọi H là giao điểm của các đường cao vừa vẽ. Chứng minh KB là tia phân giác của ∠ LKI

Những câu hỏi liên quan
Cho tam giác ABC có ba góc nhọn. Vẽ các đường cao AI, BK, CL của tam giác ấy. Gọi H là giao điểm của các đường cao vừa vẽ. Chứng minh ∠ LBH, ∠ LIH, ∠ KIH, và ∠ KCH là 4 góc bằng nhau.
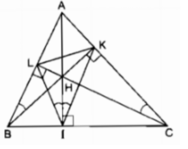
Vì ∆ ABC là tam giác nhọn nên ba đường cao cắt nhau tại điểm H nằm trong tam giác ABC.
Tứ giác BIHL nội tiếp.

Tứ giác CIHK nội tiếp.

Từ (1), (2) suy ra:
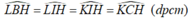
Đúng 0
Bình luận (0)
Cho tam giác ABC có ba góc nhọn. Vẽ các đường cao AI, BK, CL của tam giác ấy. Gọi H là giao điểm của các đường cao vừa vẽ. Chỉ ra các tứ giác nội tiếp có đỉnh lấy trong số các điểm A, B, C, H, I, K, L
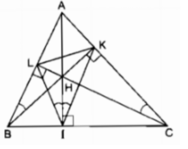
Vì ∆ ABC là tam giác nhọn nên ba đường cao cắt nhau tại điểm H nằm trong tam giác ABC.
Tứ giác AKHL có ![]()
Tứ giác AKHL nội tiếp.
Tứ giác BIHL có ![]()
Tứ giác BIHL nội tiếp.
Tứ giác CIHK có ![]()
Tứ giác CIHK nội tiếp.
Tứ giác ABIK có ![]()
K và I nhìn đoạn AB dưới một góc vuông nên tứ giác ABIK nội tiếp. Tứ giác BCKL có ![]()
K và L nhìn đoạn BC dưới một góc vuông nên tứ giác BCKL nội tiếp.
Tứ giác ACIL có 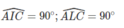
I và L nhìn đoạn AC dưới một góc vuông nên tứ giác ACIL nội tiếp.
Đúng 0
Bình luận (0)
Cho tam giác ABC có 3 góc nhọn. Vẽ các đường cao AI, BK, CL của tam giác ấy. Gọi H là giao điểm của các đường cao vừa vẽ
a) Chỉ ra các tứ giác nội tiếp có đỉnh lấy trong số các điểm A, B, C, H, I, K, L
b) Chứng minh \(\widehat{LBH},\widehat{LIH},\widehat{KIH},\widehat{KCH}\) là bốn góc bằng nhau
cho tam giác abc có 3 góc nhọn nội tiếp đường tròn (o) vẽ các đường cao be,cf của tam giác ấy gọi h là giao điểm của be và cf kẻ đg kính bk của (o)
a) Chứng minh tứ giác BCEF là tứ giác nội tiếp
b) chứng minh tứ giác AHCK là hình bình hành
c)đường tròn đường kính AC cắt BE ở M đường tròn đường kính AB cặt CF ở N.chứng minh AM=AN
a: Xét tứ giác BFEC có góc BFC=góc BEC=90 độ
nên BFEC là tứ giác nội tiếp
b: Xét (O) có
ΔBCK nội tiếp
BK là đường kính
Do đó: ΔBCK vuông tại C
=>CK//AH
Xét (O) có
ΔBAK nội tiếp
BK là đường kính
Do đó: ΔBAK vuông tại A
=>AK//CH
Xét tứ giác CHAK có
CH//AK
CK//AH
DO đó: CHAK là hình bình hành
Đúng 0
Bình luận (0)
1. Cho tam giác ABC, góc A 120 độ, đường phân giác AD. Đường phân giác góc ngoài tại C cắt đường thẳng AB ở K. Gọi E là giao điểm của DK và AC. Tính số đo của góc BED.2. Cho tam giác ABC có BC 17cm, CA 15cm, AB 8cm. Ba đường phân giác của tam giác cắt nhau tại O. Tính tổng các khoảng cách từ O đến ba cạnh của tam giác.3. Cho tam giác ABC vuông cân tại A, M là trung điểm của BC. Gọi D là điểm thuộc đoạn MC, H là hình chiếu của B trên AD. Chứng minh HM là tia phân giác của góc BHD.4. Cho tam g...
Đọc tiếp
1. Cho tam giác ABC, góc A = 120 độ, đường phân giác AD. Đường phân giác góc ngoài tại C cắt đường thẳng AB ở K. Gọi E là giao điểm của DK và AC. Tính số đo của góc BED.
2. Cho tam giác ABC có BC = 17cm, CA = 15cm, AB = 8cm. Ba đường phân giác của tam giác cắt nhau tại O. Tính tổng các khoảng cách từ O đến ba cạnh của tam giác.
3. Cho tam giác ABC vuông cân tại A, M là trung điểm của BC. Gọi D là điểm thuộc đoạn MC, H là hình chiếu của B trên AD. Chứng minh HM là tia phân giác của góc BHD.
4. Cho tam giác ABC và điểm I là giao điểm 3 đường phân giác của tam giác. Gọi H là chân đường vuông góc kẻ từ B đến AI. Chứng minh rằng góc IBH = góc ICA.
5. Cho tam giác ABC có góc B = 50 độ, góc C = 20 độ, đường cao AH. Tia phân giác của góc AHC cắt AC tại D. Vẽ tia Ax là tia đối của tia AB. Chứng minh điểm D nằm trên tia phân giác của góc ABC.
cho tam giác ABC nhọn (AB>AC) có góc B bằng 45 độvà vẽ đường cao AH. Gọi M là trung điểm AB. P là điểm dối xúng với H qua M. a, Chứng minh AHBP là hình vuông b, Vẽ đường cao BK của tam giác ABC. Chứng minh HP=2MK c, Gọi D là giao điểm của AH và BK. Qua D và C vẽ các đường thẳng song song với BC và AH sao cho chúng cắt nhau tại Q. Chứng minh P,K,Q tahwngr hàng
cho tam giác ABC (AB<AC) có ba góc nhọn nội tiếp đường tròn (o). các đường cao AD,BE của tam giác ABC cắt nhau tại H
a) c/m tứ giác ABDE nội tiếp
b) trong đường tròn (o) vẽ đường kính AK gọi N là giao điểm của AD vad BK chứng minh EM/DN = EH/DH
c) DE cắt MN tại I chứng minh IM=IN
a: góc AEB=góc ADB=90 độ
=>AEDB nội tiếp
b,c: M ở đâu vậy bạn?
Đúng 0
Bình luận (0)
Cho tam giác ABC có 3 góc nhọn, vẽ các đường cao BD,CE cắt nnhau tại H. gọi K là giao điểm của AH với BC.cm BD là tia phân giác của góc EDK
Cho tam giác ABC có ba góc nhọn, nội tiếp đường tròn (O). Vẽ các
đường cao BE, CF của tam giác ấy. Gọi H là giao điểm của BE và CF. Kẻ đường kính
BK của (O) .
a) Chứng minh tứ giác BCEF là tứ giác nội tiếp.
b) Chứng minh tứ giâc AHCK là mình bình hành.
c) Đường tròn đường kính AC cắt BE ở M, đường tròn đường kính AB cặt CF ở N.
Chứng minh AM =AN .














