Viết phương trình tiếp tuyến của đồ thị hàm số y = − x 3 + 3 x + 1 tại giao điểm của đồ thị với trục tung.
A. y = 1
B. y = 3x - 1
C. y = 3x + 1
D. y = -3x + 1
a) tìm hệ số góc của tiếp tuyến của đồ thị hàm số y=-x^3+3x-2 (c) tại điểm có hoành độ -3
b) viết phương trình tiếp tuyến của đồ thị hàm số (c) trên tại điểm ( ứng với tiếp điểm ) có hoành độ -3
Viết phương trình tiếp tuyến của đồ thị hàm số y = x - 1 x + 2 tại điểm có hoành độ x=-3
A. y=-3x-5
B. y=-3x+13
C. y=3x+13
D. y=3x+5
viết phương trình tiếp tuyến của đồ thị hàm số y=x^3 -3x 4 tiếp tuyến vuông góc với đường thẳng d:y-1/3x 4=0
Ủa trước 2 số 4 kia là dấu gì vậy bạn?
\(y'=3x^2-3\)
Phương trình d: \(y-\dfrac{1}{3}x-4=0\Leftrightarrow y=\dfrac{1}{3}x+4\)
Gọi k là hệ số góc của tiếp tuyến, do tiếp tuyến vuông góc d nên:
\(k.\left(\dfrac{1}{3}\right)=-1\Rightarrow k=-3\)
Gọi \(x_0\) là hoành độ tiếp điểm \(\Rightarrow y'\left(x_0\right)=k\)
\(\Rightarrow3x^2_0-3=-3\)
\(\Rightarrow x_0=0\)
\(\Rightarrow y_0=x_0^3-4x_0+4=4\)
Phương trình tiếp tuyến:
\(y=-3\left(x-0\right)+4\Leftrightarrow y=-3x+4\)
Viết phương trình tiếp tuyến của đồ thị hàm số \(y = {x^3} + 3{x^2} - 1\) tại điểm có hoành độ bằng 1.
Ta có: \(y'=3x^2+6x\Rightarrow\left\{{}\begin{matrix}y'\left(1\right)=9\\y\left(1\right)=3\end{matrix}\right.\)
Phương trình tiếp tuyến là: \(y=9\left(x-1\right)+3=9x-6\)
a) Tính đạo hàm của hàm số \(y=\sqrt{sinx+cosx}\)
b) Hãy viết phương trình tiếp tuyến với đồ thị (C) của hàm số \(y=\dfrac{x+3}{x-1}\) biết tiếp tuyến vuông góc với đường thẳng \(y=\dfrac{1}{4}x+5\)
a.
\(y'=\dfrac{\left(sinx+cosx\right)'}{2\sqrt{sinx+cosx}}=\dfrac{cosx-sinx}{2\sqrt{sinx+cosx}}\)
b.
\(y'=\dfrac{-4}{\left(x-1\right)^2}\)
Tiếp tuyến vuông góc với \(y=\dfrac{1}{4}x+5\) nên có hệ số góc thỏa mãn \(k.\left(\dfrac{1}{4}\right)=-1\Rightarrow k=-4\)
\(\Rightarrow\dfrac{-4}{\left(x-1\right)^2}=-4\Rightarrow\left(x-1\right)^2=1\)
\(\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y=-3\\x=2\Rightarrow y=5\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}y=-4x-3\\y=-4\left(x-2\right)+5\end{matrix}\right.\)
Cho hàm số y = x 3 + 3 x 2 - 2 x - 3 có đồ thị (C). Viết phương trình tiếp tuyến của đồ thị (C) biết tiếp tuyến có hệ số góc nhỏ nhất.
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Đáp án C
![]() , y’ đạt giá trị nhỏ nhất bằng –5 tại x = –1.
, y’ đạt giá trị nhỏ nhất bằng –5 tại x = –1.
Cho hàm số y = x 3 + 3 x 2 - 2 x - 3 có đồ thị (C). Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến có hệ số góc nhỏ nhất.
A. y=7x-8
B. y=-5x-4
C. y= -5x+6
D. y=7x+6
Cho đồ thị hàm số C : y = − 2 x + 3 x − 1 . Viết phương trình tiếp tuyến của đồ thị (C) tại
giao điểm của (C) và đường thẳng y = x − 3 .
A. y = − x + 3 v à y = − x − 1
B. y = − x − 3 v à y = − x + 1
C. y = x − 3 v à y = x + 1
D. y = − x + 3 v à y = − x + 1
Đáp án B
Tọa độ giao điểm của (C) và đường thẳng y = x − 3 là nghiệm của hệ:
y = − 2 x + 3 x − 1 y = x − 3 ⇔ x = 2 y = − 1 x = 0 y = − 3 ⇒ A ( 2 ; − 1 ) B ( 0 ; − 3 )
y ' = − 1 x − 1 2
Phương trình tiếp tuyến với ( C) tại A ( 2 ; − 1 ) là:
y = − 1 2 − 1 2 ( x − 2 ) − 1 = − x + 1
Phương trình tiếp tuyến với ( C) tại B ( 0 ; − 3 ) là:
y = − 1 0 − 1 2 ( x − 0 ) − 3 = − x − 3
Cho hàm số y = x - 1 x + 1 . Viết phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến song song với d : y = x - 2 2
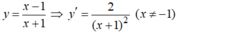
d: 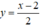 có hệ số góc k = 1/2 ⇒ Tiếp tuyến có hệ số góc k = 1/2.
có hệ số góc k = 1/2 ⇒ Tiếp tuyến có hệ số góc k = 1/2.
- Gọi ( x 0 , y 0 ) là toạ độ của tiếp điểm.
- Ta có:
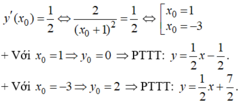
viết phương trình tiếp tuyến với đồ thị hàm số y=\(x^3-3x+1\) tại M(2,3)
Ta có \(y'=3x^2-3\Rightarrow k=y'\left(2\right)=9\).
Phương trình tiếp tuyến tại M(2; 3) là:
\(d:y=y_0'\left(x-x_0\right)+y_0\Leftrightarrow y=9\left(x-2\right)+3\Leftrightarrow y=9x-15\).