Cho một cấp số nhân có các số hạng đều không âm thỏa mãn u 2 = 6 , u 4 = 24. Tính tổng của 12 số hạng đầu tiên của cấp số nhân đó.
A. 3.2 12 − 3.
B. 2 12 − 1.
C. 3.2 12 − 1.
D. 3.2 12 .
Cho một cấp số nhân có các số hạng đều không âm thỏa mãn u 2 = 6 , u 4 = 24 . Tính tổng của 12 số hạng đầu tiên của cấp số nhân đó
A. 3 . 2 12 - 3
B. 2 12 - 1
C. 3 . 2 12 - 1
D. 3 . 2 12
Có bao nhiêu bộ bốn số thỏa mãn ba số hạng đầu lập thành một cấp số nhân, ba số hạng sau lập thành một cấp số cộng; tổng của hai số hạng đầu và cuối bằng 14, còn tổng của hai số ở giữa là 12?
A. 1
B. 2
C. 3
D. 4
Cho hai cấp số nhân có cùng số các số hạng. Tích các số hạng tương ứng của chúng có lập thành cấp số nhân không? Vì sao? Cho một ví dụ minh họa.
Giả sử có hai cấp số nhân (un) với công bội q1 và (vn) với công bội q2.
Xét dãy số (an) với an = un.vn với mọi n ∈ N*.
Ta có:
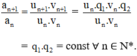
⇒ (an) là cấp số nhân với công bội q1.q2.
Ví dụ:
+ CSN (un) : 2 ; 4 ; 8 ; 16 ; 32 ; 64 ; … có công bội q1 = 2.
+ CSN (vn) : -1 ; 1 ; -1 ; 1 ; -1 ; 1 ; … có công bội q2 = -1.
⇒ CSN (an) : -2 ; 4 ; -8 ; 16 ; -32 ; 64 ; … có công bội q = -2.
Một cấp số cộng và một cấp số nhân đều là các dãy số tăng. Các số hạng thứ nhất đều bằng 3, các số hạng thứ hai bằng nhau, tỷ số giữa các số hạng thứ ba của cấp số nhân và cấp số cộng là 9/5. Tính tổng S của cấp số nhân đó
A. S= 27
B. S= 39
C. S= 29
D. S= 37
Cho hai cấp số nhân có cùng số các số hạng. Tích các số hạng tương ứng của chúng có lập thành cấp số nhân không ? Vì sao ? Cho một ví dụ minh họa ?
an= a1. q1n-1, q1 là hằng số
bn= \(b_1q_2^{n-1}\), q2 là hằng số
Khi đó: an.bn = = a1. q1n-1. b1. q1n-1 = (a1b1)(q1q2)n-1
Vậy dãy số anbn là một cấp số nhân có công bội : q = q1q2
Ví dụ:
1, 2, 4 ,... là cấp số nhân có công bội q1 = 2
3, 9, 27, .... là cấp số nhân có công bội q2 = 3
⇒ Suy ra: 3, 8, 108.. là cấp số nhân có công bội: q = q1q2 = 2.3 = 6
Một cấp số cộng và một cấp số nhân đều là các dãy tăng. Các số hạng thứ nhất đều bằng 3, các số hạng thứ hai bằng nhau. Tỉ số giữa số hạng thứ ba của cấp số nhân và cấp số cộng là 9/5. Tính tổng các số hạng thứ ba của hai cấp số trên.
A. 29.
B. 24.
C. 18.
D. 42.
Cho cấp số nhân u n thỏa mãn u 1 + u 2 + u 3 = 13 u 4 − u 1 = 26 . Tổng 8 số hạng đầu của cấp số nhân u n là
A. S 8 = 1093.
B. S 8 = 3820
C. S 8 = 9841
D. S 8 = 3280
Cho cấp số nhân thỏa mãn u1+u2+u3=13;u4-u1=26 . Tổng 8 số hạng đầu của cấp số nhân (un) là
\(\left\{{}\begin{matrix}u1+u2+u3=13\\u4-u1=26\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u_1+u_1\cdot q+u_1\cdot q^2=13\\u_1\cdot q^3-u_1=26\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u_1\left(1+q+q^2\right)=13\\u_1\left(q^3-1\right)=26\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1+q+q^2}{\left(q-1\right)\left(q^2+q+1\right)}=\dfrac{13}{26}=\dfrac{1}{2}\\u_1\left(q^3-1\right)=26\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{q-1}=\dfrac{1}{2}\\u_1\left(q^3-1\right)=26\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}q-1=2\\u_1=\dfrac{26}{q^3-1}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}q=2+1=3\\u_1=\dfrac{26}{3^3-1}=1\end{matrix}\right.\)
Tổng 8 số hạng đầu của cấp số nhân là:
\(\dfrac{u_1\left(1-q^8\right)}{1-q}=\dfrac{1\cdot\left(1-3^8\right)}{1-3}=3280\)
\(\left\{{}\begin{matrix}u_1+u_2+u_3=13\\u_4-u_1=26\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}u_1+u_1.q+u_1.q^2=13\\u_1.q^3-u_1=26\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}u_1\left(1+q+q^2\right)=13\\u_1\left(q^3-1\right)=26\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}u_1\left(1+q+q^2\right)=13\\u_1\left(q-1\right)\left(q^2+q+1\right)=26\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}13.\left(q-1\right)=26\\u_1.\left(q^3-1\right)=26\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}q=3\\u_1=1\end{matrix}\right.\)
\(S_8=\dfrac{u_1\left(1-q^8\right)}{1-q}=\dfrac{1.\left(1-3^8\right)}{1-3}=3280\)
Cho cấp số nhân (un) thỏa mãn: u 4 = 2 27 u 3 = 243 u 8 . Số 2 6561 là số hạng thứ bao nhiêu của cấp số ?
A. 11
B. 12
C. 6
D. 9
Chọn D
Gọi q là công bội của cấp số. Theo giả thiết ta có
u 1 q 3 = 2 27 u 1 q 2 = 243. u 1 q 7 ⇔ u 1 q 3 = 2 27 q 5 = 1 243 ⇔ q = 1 3 u 1 = 2
Ta có:
u n = 2 3 n − 1 ⇒ u n = 2 6561 ⇔ 3 n − 1 = 6561 = 3 8 ⇒ n = 9
Vậy 2 6561 là số hạng thứ 9 của cấp số.