Cho tứ diện ABCD có BC=a, C D = a 3 , B C D ^ = A B C ^ = A D C ^ = 90 ° . Góc giữa hai đường thẳng AD và BC bằng 60 ° . Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABCD.
A. a 3 2
B. a 3
C. a
D. a 7 2
Những câu hỏi liên quan
Tứ diện ABCD. Các điểm A'B'C'D' là điểm chia AB, BC, CD, DA theo tỉ số k (k≠1). Chứng minh tứ diện ABCD và tứ diện A'B'C'D' có cùng trọng tâm
Cho tứ giác ABCD có ^A = ^B=90° a) cm AB//BC b) cho ^D = 3^C. Tính ^C, ^D
a) Sửa đề: AD//BC
Ta có: AD\(\perp\)AB(gt)
BC\(\perp\)AB(gt)
Do đó: AD//BC(Định lí 1 từ vuông góc tới song song)
b) Ta có: AD//BC(cmt)
nên \(\widehat{D}+\widehat{C}=180^0\)(hai góc trong cùng phía)
\(\Leftrightarrow4\cdot\widehat{C}=180^0\)
hay \(\widehat{C}=45^0\)
Ta có: \(\widehat{D}=3\cdot\widehat{C}\)
nên \(\widehat{D}=135^0\)
Đúng 0
Bình luận (0)
Cho tứ giác ABCD vuông ở C và D, có AD = 6 cm BC = 9 cm DC = 8 cm Nối A với C, B với D.
A, Tính diện tích tam giác ABC
B,Hãy so sánh diện tích ADC và BDC.
Cho hình tứ diện ABCD có AB, BC, CD đôi một vuông góc. Điểm cách đều bốn điểm A, B, C, D là:
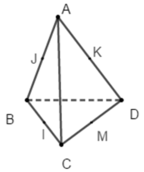
A. trung điểm J của AB
B. trung điểm I của BC
C. trung điểm K của AD
D. trung điểm M của CD
CD ⊥ (ABC) vì CD ⊥ AB và CD ⊥ BC
AB ⊥ (BCD) vì AB ⊥ BC và AB ⊥ CD
Phương án A sai vì tam giác ABC không vuông góc tại C nên trung điểm của AB không cách đều ba điểm A, B, C
Phương án B sai vì tam giác ABC không vuông góc tại A nên trung điểm của BC không cách đều ba điểm A, B, C
Phương án C đúng vì tam giác ACD vuông góc tại C nên trung điểm K của AD cách đều ba điểm A, C, D; tam giác ABD vuông góc tại B nên trung điểm K của AD cách đều ba điểm A, B và D
Phương án D sai vì tam giác CBD không vuông góc tại B nên trung điểm của CD không cách đều ba điểm B, C, D.
Đáp án C
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có góc A=góc B=90 độ a)Cm AD//BC b)Cho D=3C.Tính C,D c)Cho D-C=30 độ.Tính C,D
a) Có AD ⊥ AB( góc A vuông)
BC ⊥ AB( góc B vuông)
=> AD // BC
b) Có tứ giác ABCD= 360 độ
mà A = B= 90 độ
=> C + D= ABCD - A - B
= 360 độ - 90 độ - 90 độ
= 180 độ
Có D = 3C và C + D = 180 độ
=> C = 45 độ
=> D = 135 độ
c) Có ABCD= 360 độ
A = B= 90 độ
=> C + D= 180 độ
=> D =180 độ - C
+) D - C = 30 độ
<=> 180 độ - C - C = 30 độ
<=> 2C= 150 độ
<=> C = 75 độ
=> D = 105 độ
Vậy a) AD // BC
b) C = 45 độ
D = 135 độ
c) C = 75 độ
D = 105 độ
Đúng 1
Bình luận (0)
Cho tứ diện ABCD có AD ⊥ (ABC) và BD ⊥ BC. Khi quay tứ diện đó xung quanh trục là cạnh AB, có bao nhiêu hình nón được tạo thành?
A. Một B. Hai
C. Ba D. Bốn
Chọn B.
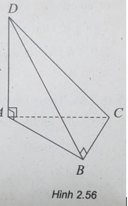
(h.2.56) Khi quay tứ diện quanh AB, AD và BC nằm trên hai mặt phẳng song song với nhau, cùng vuông góc với AB lần lượt tại A và B. Ta có hai hình nón: Hình nón đỉnh A, đường cao AB, bán kính đáy là BC. Hình nón đỉnh B, đường cao BA, bán kính đáy là AD.
Đúng 0
Bình luận (0)
cho tam giác cân ABC có AM là đường trung tuyến biết AB = 15 cm BC = 18.Gọi D đối xứng với A qua BC. Diện tích tứ giác ABCD là: A: 108cm2 B: 216cm2 C: 270cm2 D: 66cm2
ta có: AB=AC( tam giác ABC cân)
=> tứ giác ABCD là hình thoi
MB=18:2=9 cm
ta có M là trung tuyến cũng là đường cao trong tam giác ABC
áp dụng định lý pitago, ta có:
\(AB^2=BM^2+AM^2\)
\(15^2=9^2+AM^2\)
=>AM=12cm
=>AD= 24cm
=> diện tích tứ giác ABCD là:
\(\dfrac{1}{2}.AD.BC\)
<=>\(\dfrac{1}{2}.24.18=216cm^2\)
Chọn B
Đúng 0
Bình luận (2)
Xem thêm câu trả lời
cho tứ giác ABCD có AB=a; BC=b; CD=c; DA=d (a,b,c,d > 0 thỏa \(a^2+b^2+c^2+d^2=\left(a+c\right)\left(b+d\right)\)
a) tứ giác ABCD có gì đặc biệt?
b) nếu cho thêm giả thiết AC*BD=ab+cd khi đó tính các góc của ABCD
a) \(a^2+b^2+c^2+d^2=ab+bc+ac+cd.\)
<=>\(2a^2+2b^2+2c^2+2d^2=2ab+2ac+2bc+2cd\)
<=>\(2a^2+2b^2+2c^2+2d^2-2ab-2bc-2ac-2cd=0\)
<=>\(\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ac+a^2\right)+\left(d^2-2cd+c^2\right)\)=0
<=>\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2+\left(d-c\right)^2=0\)
=>a=b=c=d
=> ABCD là hình thoi
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có AD\(\perp\)(ABC),độ dài các cạnh BC,AC,AB,AD lần lượt là a,b,c,d đáy ABC thỏa mãn điều kiện \(\dfrac{cotA+cotB+cotC}{2}=\dfrac{BC}{AB.AC}+\dfrac{CA}{BC.BA}+\dfrac{AB}{CA.CB}\).Tính thể tích V của tứ diện ABCD theo a,b,c,d
Cho tứ giác ABCD . Kéo dài cạnh AB về phía B một đoạn BB' bằng 2 lần AB . Kéo dài cạnh BC về phía C một đoạn CC' bằng 2 lần BC . Kéo dài CD về phía D một đoạn DD' bằng 2 lần CD và kéo dài cạnh DA về phía A một đoạn AA' bằng 2 lần DA . Nối A 'B' , B 'C' , C 'D' , D 'A' .
Hãy tính diện tích tứ giác A'B'C'D . Biết diện tích tứ giác ABCD đã cho là 450 cm2 .
