Tìm giá trị của m để hàm số y = x + m(sinx + cosx + m ) luôn đồng biến trên R
A. - 2 2 ≤ m ≤ 2 2
B. 0 ≤ m ≤ 2 2
C. - 2 2 ≤ m ≤ 0
D. - 2 ≤ m ≤ 2
Có bao nhiêu giá trị nguyên của m để hàm số y=3x+m(sinx + cosx +m) đồng biến trên R?
A. 5
B. 4
C. 3
D. Vô số
Có bao nhiêu giá trị nguyên của m để hàm số y = 3x + m(sinx+cosx+m) đồng biến trên R?
A. 5
B. 4
C. 3
D. vô số
Đáp án A
Ta có: ![]()
Hàm số đồng biến trên R khi ![]()
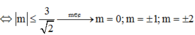
Vậy có 5 giá trị nguyên của m
Có bao nhiêu giá trị nguyên dương của m để hàm số y= 3x+ m(sinx+ cosx+m) đồng biến trên R ?
A. 5
B. 4
C. 3
D. 2
Đạo hàm : y ' = 3 + m ( cos x - sin x ) = 3 + m 2 cos ( x + π 4 )
Hàm số đồng biến trên R khi y’ ≥ 0 với mọi x
⇔ M i n ℝ y ' ≥ 0 ⇔ 3 - m 2 ≥ 0 ⇔ m ≤ 3 2 → m ∈ ℤ m = 0 ; m = ± 1 ; m = ± 2 .
Vậy có 2 giá trị nguyên dương của m thỏa mãn đầu bài.
Chọn D.
Cho hàm số y=sinx- 3 cosx-mx Tìm tất cả các giá trị thực của tham số m để hàm số đồng biến trên R.
A.![]()
B.m>2
C.![]()
D.![]()
Tìm tất cả các giá trị thực m để hàm số y=sinx+cosx+mx đồng biến trên R.
A.![]() .
.
B.![]() .
.
C.![]() .
.
D.![]() .
.
Chọn C
Ta có ![]()
![]() .
.
Vì ![]()
![]()
![]() .
.
![]()
![]() .
.
Để hàm số đã cho đồng biến trên ![]()
![]()
![]() ,
, ![]() .
.
![]()
![]()
![]()
![]() .
.
Tìm tất cả các giá trị của để hàm số y = x + m ( sin x + cos x ) đồng biến trên ℝ
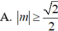
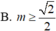
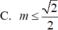
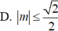
Với giá trị nào của tham số m thì hàm số y = sin x - cos x + 2017 2 m x đồng biến trên R.
A. m ≥ 2017
B. 1
C. m ≥ 1 2017
D. m ≥ - 1 2017
+ Tính đạo hàm y ' = cos x + sin x + 2017 2 m .
y ' ≥ 0 ⇔ m ≥ - sin x - cos x 2017 2 = f ( x )
+ Theo bất đẳng thức Bunhiacopxki thì
( - sin x - cos x ) 2 ≤ ( - 1 ) 2 + ( - 1 ) 2 sin 2 x + cos 2 x = 2 - 2 ≤ ( - sin x - cos x ) ≤ 2
Do đó :
- 2 2017 2 ≤ f ( x ) ≤ 2 2017 2
F(x) đạt giá trị lớn nhất là 2 2017 2 = 1 2017 ⇒ m ≥ f ( m a x ) = 1 2017
Chọn C.
Tìm tất cả các giá trị thực của m để hàm số y = ( m 2 + m + 1 ) x + ( m 2 - m + 1 ) sin x luôn đồng biến trên ( 0 ; 2 π )
A. m ≤ 0
B. m ≥ 0
C. m > 0
D. m < 0
Tìm tất cả các giá trị của tham số m để hàm số y = x + m ( sin x + c o s x ) đồng biến trên R
A. m < - 1 2 ∪ m > 1 2
B. - 1 2 ≤ m ≤ 1 2
C. - 3 < m < 1 2
D. m ≤ - 1 2 ∪ m ≥ 1 2