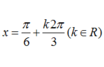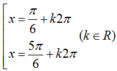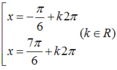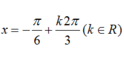+ Tính đạo hàm y ' = cos x + sin x + 2017 2 m .
y ' ≥ 0 ⇔ m ≥ - sin x - cos x 2017 2 = f ( x )
+ Theo bất đẳng thức Bunhiacopxki thì
( - sin x - cos x ) 2 ≤ ( - 1 ) 2 + ( - 1 ) 2 sin 2 x + cos 2 x = 2 - 2 ≤ ( - sin x - cos x ) ≤ 2
Do đó :
- 2 2017 2 ≤ f ( x ) ≤ 2 2017 2
F(x) đạt giá trị lớn nhất là 2 2017 2 = 1 2017 ⇒ m ≥ f ( m a x ) = 1 2017
Chọn C.
Cho hàm số y = 1 3 x 3 - m x 2 + ( 4 m - 3 ) x + 2017 . Tìm giá trị lớn nhất của tham số thực m để hàm số đã cho đồng biến trên .
A. m = 2
B. m = 3
C. m = 4
D. m = 1
cho hàm số y = \(\left(\frac{4}{2017}\right)^{e^{3x}-\left(m-1\right)e^x+1}\)Tìm m đểhàm số đồng biến trên (1; 2)
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x ( 2017 + 2019 - x 2 ) trên tập xác định của nó. Tính M-m.
A. 
.
B. 
.
C. 
.
D. 
.
Gọi M, m lần lượt là giá trị lớn nhất , giá trị nhỏ nhất của hàm số y = x(2017 +\(\sqrt{2019-x^2}\)) trên tập xác định của nó . Tính M-m
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y= (m-3)x- (2m+1).cos x luôn nghịch biến trên R?
A. - 4 ≤ m ≤ 2 3
B. m> 2
C. m > 3 m ≠ 1
D. m<2
Tìm tất cả giá trị thực của tham số m để hàm số y = x 3 3 + ( m + 1 ) x 2 + ( 3 m + 1 ) x + 2 đồng biến trên R
A.
B.
C. 
D. 
Cho hàm số: y = –( m 2 + 5m) x 3 + 6m x 2 + 6x – 5
a) Xác định m để hàm số đơn điệu trên R. Khi đó, hàm số đồng biến hay nghịch biến? Tại sao?
b) Với giá trị nào của m thì hàm số đạt cực đại tại x = 1 ?
Tìm tập các giá trị của tham số m để hàm số y = x 3 3 + x 2 + ( m - 1 ) x + 2018 đồng biến trên R.
A. [-1;+ ∞ )
B. [1;2]
C. (- ∞ ;2]
D. [2;+ ∞ )
Cho hàm số f ( x ) = a x 4 + b x 2 + c v ớ i a > 0 , c > 2017 , a + b + c < 2017 . Số cực trị của hàm số y = | f ( x ) - 2017 | là
A. 1
B. 5
C. 3
D. 7
Tìm tất cả các điểm cực trị của hàm số y = 1/2.sin 2x + cos x – 2017
A. 
B. 
C. 
D. 
