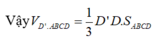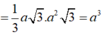Cho khối hộp ABCD . A ' B ' C ' D ' . Tính tỉ số thể tích của khối tứ diện ABDA ' và khối hộp ABCD . A ' B ' C ' D ' .
A. 6.
B. 1 6
C. 1 3
D. 1 2
Cho hình hộp đứng ABCD.A¢B¢C¢D¢ có AB = a, AD = 2 a , BD = a 3 . Góc tạo bởi AB¢ và mặt phẳng (ABCD) bằng 60 o . Tính thể tích của khối chóp D¢.ABCD.
A. 3 3 a 3 .
B. 3 a 2 .
C. a 3 .
D. 2 3 3 a 3 .
Hình hộp đứng ABCD.A′B′C′D′ có đáy là hình thoi. Diện tích các tứ giác ABCD,ACC′A′,BDD′B′ lần lượt là S 1 , S 2 , S 3 . Khi đó thể tích khối hộp ABCD.A′B′C′D′ là
A. 1 3 S 1 S 2 S 3
B. 1 2 S 1 S 2 S 3
C. 1 3 S 1 S 2 S 3
D. 1 2 S 1 S 2 S 3
cho hình hộp chữ nhật ABCD, A'B'C'D' mệnh đề nào sau đây đúng?
A) (ABCD) ⊥ (ABB ' A').
B) (ABCD) ⊥ (A' BD).
C. (ABB' A') ⊥ (CDD'C').
D. (ABCD) ⊥ (A'B'C'D').
\(\left\{{}\begin{matrix}BB'\perp\left(ABCD\right)\\BB'\in\left(ABB'A'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(ABB'A'\right)\)
Khối hộp chữ nhật ABCD.A'B'C'D' có diện tích các mặt ABCD,ABB' A',ADD' A' lần lượt =20cm vuông,28cm vuông,35 cm vuông.Thể tích của khối hộp chữ nhật đó bằng
Cho hình hộp đứng \(ABCD.A'B'C'D'\) có cạnh bên \(AA' = 2a\) và đáy \(ABCD\) là hình thoi có \(AB = a\) và \(AC = a\sqrt 3 \).
a) Tính khoảng cách giữa hai đường thẳng \(B{\rm{D}}\) và \(AA'\).
b) Tính thể tích của khối hộp.
a) Gọi \(O = AC \cap B{\rm{D}}\)
\(ABCD\) là hình thoi \( \Rightarrow AC \bot B{\rm{D}} \Rightarrow AO \bot B{\rm{D}}\)
\(AA' \bot \left( {ABCD} \right) \Rightarrow AA' \bot AO\)
\( \Rightarrow d\left( {B{\rm{D}},AA'} \right) = AO = \frac{1}{2}AC = \frac{{a\sqrt 3 }}{2}\)
b) Tam giác \(OAB\) vuông tại \(O\)
\(\begin{array}{l} \Rightarrow BO = \sqrt {A{B^2} - A{O^2}} = \frac{a}{2} \Rightarrow B{\rm{D}} = 2BO = a\\{S_{ABC{\rm{D}}}} = \frac{1}{2}AC.B{\rm{D}} = \frac{{{a^2}\sqrt 3 }}{2}\\{V_{ABC.A'B'C'}} = {S_{ABC{\rm{D}}}}.AA' = \frac{{3{a^3}}}{4}\end{array}\)
Cho hình hộp chữ nhật ABCD. A'B'C'D' có AB bằng a. Diện tích của ABCD va ABC'D' lần có AA'=a√2, AB=a; A'C=3a. Tính thể tích hình hộp chữ nhật
Xét khối hộp ABCDA’B’C’D’, trong đó ABCD là hình thôi có các đường chép bằng a và 2a ; cạnh bên AA’=2a và tạo với mặt phẳng góc bằng 30o . Tính thể tích khối hộp
Tính thể tích V của khối hộp ABCDA’B’C’D’, trong đó A’ABD là tứ diện đều cạnh a.
Tính thể tích V của khối chóp tam giác SABCD, trong đó SABC là tứ diện đều cạnh á và ABCD là hình thoi
a/ Diện tích đáy: \(S=\frac{1}{2}.a.2a=a^2\)
Độ dài đường cao: \(h=AA'.sin30^0=a\)
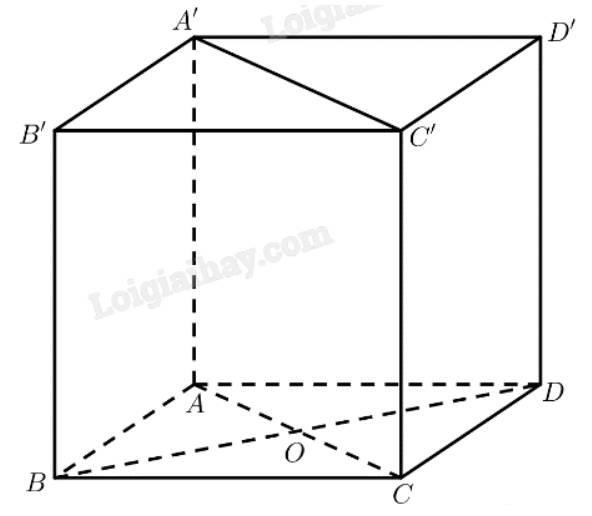
\(\Rightarrow V=S.h=a^3\)
b/ Diện tích đáy: \(S=2.\frac{a^2\sqrt{3}}{4}=\frac{a^2\sqrt{3}}{2}\)
Độ dài đường cao: \(h=\frac{a\sqrt{6}}{3}\)
\(\Rightarrow V=S.h=\frac{a^3\sqrt{2}}{2}\)
c/ Diện tích đáy: \(S=2.\frac{a^2\sqrt{3}}{4}=\frac{a^2\sqrt{3}}{2}\)
Độ dài đường cao: \(h=\frac{a\sqrt{6}}{3}\)
\(\Rightarrow V=\frac{1}{3}S.h=\frac{a^3\sqrt{2}}{6}\)
Cho hình hộp ABCD.A’B’C’D’ có AB =a, BB'= a 5 các đường thẳng A’B và B’C cùng tạo với mặt phẳng (ABCD) một góc 45 0 tam giác A’AB vuông tại B, tam giác A’CD vuông tại D. Tính thể tích của khối hộp ABCD.A’B’C’D’ theo a
A. 2 a 3
B. 2 a 3 3
C. a 3 6 2
D. a 3 6 6
Cho hình hộp ABCD.A’B’C’D’ có AB=A,B'C'= a 5 các đường thẳng A’B và B’C cùng tạo với mặt phẳng (ABCD) một góc 45 ° tam giác A’AB vuông tại B, tam giác A’CD vuông tại D. Tính thể tích của khối hộp ABCD.A’B’C’D’ theo a
A. 2 a 3
B. 2 a 3 3
C. a 3 6 2
D. a 3 6 6
Đáp án A
Theo giả thết ta có: ∆ A A ' B ⊥ ⇒ A B ⊥ A ' B ∆ A ' C D ⊥ ⇒ C D ⊥ A ' D ⇒ A B ⊥ A ' D ⇒ A B ⊥ ( A ' B D ) ⇒ A B ⊥ B D ⇒ B D = A D 2 - A B 2 = 5 a 2 - a 2 = 2 a ⇒ S A B C D = 2 S A B D = A B . A D = a . 2 a = 2 a 2
Kẻ đường cao AH trong ∆ A'BD , góc giữa AB' và (ABCD) là góc A'BH= 45 °
Do B'C // A'D nên góc giữa B'C và (ABCD) là góc A'DH= 45 ° ⇒ ∆ A ' B D vuông cân ⇒ A ' H = B D 2 = 2 a 2 = a từ đây tính được V A B C D . A ' B ' C ' D ' = A ' H . S A B C D = a . 2 a 2 = 2 a 3
Cho hình hộp đứng ABCD.A'B'C'D' có AB = a, AD = 2a, BD = a 3 . Góc tạo bởi AB' và mặt phẳng (ABCD) bằng 60 0 Tính thể tích của khối chóp D'.ABCD.
A. 3 a 3 3
B. 3 a 3
C. a 3
D. 2 3 a 3 3
Đáp án là C
Xét hình bình hành ABCD
![]()
suy ra tam giác ABD vuông tại B , suy ra
![]()
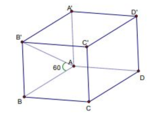
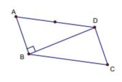
Góc giữa AB' và mặt phẳng ( ABCD) bằng B'AB nên B'AB = 60 0
Suy ra
![]()