Tổng các nghiệm của phương trình 3 x + 1 + 3 1 - x = 10 là
A. 1
B. 0
C. -1
D. 3
Tổng bình phương các nghiệm của phương trình 2 x + 1 + 3 − x = 1 + 3 + 2 x − x 2
A. 4
B. 8
C. 10
D. 9
Điều kiện: x + 1 ≥ 0 3 − x ≥ 0 x + 1 + 3 − x ≠ 0 ⇔ x ≥ − 1 x < 3 ⇔ − 1 ≤ x ≤ 3
Đặt: x + 1 + 3 − x = t t > 0
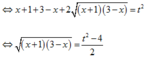
Khi đó, phương trình trở thành: 2 t = 1 + t 2 − 4 2 ⇔ 2 t = t 2 − 2 2
⇔ t 3 − 2 t − 4 = 0 ⇔ t − 2 t 2 + 2 t + 2 = 0 ⇔ t = 2
+ Với t = 2
⇔ x + 1 3 − x = 0 ⇔ x + 1 3 − x = 0 ⇔ x = − 1 ( t m ) x = 3 ( t m )
Tổng bình phương các nghiệm là: 10
Đáp án cần chọn là: C
Biết x=-3 là một nghiệm của phương trình -2x2+m-1.x+m=0( với m là tham số). Tổng các nghiệm của phương trình
Theo đề, ta có:
-2(-3)^2+(m-1)*(-3)+m=0
=>-3m+3+m-2*9=0
=>-2m-15=0
=>m=-15/2
PT khi đó sẽ là -2x^2+(-17/2)x-15/2=0
=>2x^2+17/2x+15/2=0
=>x=-5/4
Tổng các nghiệm là -5/4-3=-17/4
Tổng các nghiệm của phương trình 3 . 9 x 2 + x - 1 - 10 . 3 x 2 + x - 1 + 3 = 0 là
A. 2
B. 0
C. 1
D. -2
Tổng bình phương các nghiệm của phương trình \(x^3+1=2\sqrt[3]{2x-1}\) trên tập số thực bằng
Đặt \(\sqrt[3]{2x-1}=t\Rightarrow2x=t^3+1\)
Ta được hệ: \(\left\{{}\begin{matrix}x^3+1=2t\\t^3+1=2x\end{matrix}\right.\)
\(\Rightarrow x^3-t^3=2t-2x\)
\(\Leftrightarrow\left(x-t\right)\left(x^2+xt+t^2\right)+2\left(x-t\right)=0\)
\(\Leftrightarrow\left(x-t\right)\left(x^2+xt+t^2+2\right)=0\)
\(\Leftrightarrow x=t\) (do \(x^2+xt+t^2+2=\left(x+\dfrac{t}{2}\right)^2+\dfrac{3t^2}{4}+2>0\))
\(\Leftrightarrow x=\sqrt[3]{2x-1}\Leftrightarrow x^3=2x-1\)
\(\Leftrightarrow x^3-2x+1=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+x-1\right)=0\)
Tới đây bấm máy hoặc dùng Viet
Tổng các nghiệm của phương trình x(x + 1)(x + 2)(x + 3) = 8 là:
A. −3
B. 3
C. 1
D. −4
Cho phương trình y = x 3 - 6 x 2 + 9 x - 2 và các phát biểu sau:
(1) x = 0 là nghiệm duy nhất của phương trình
(2) Phương trình có nghiệm dương
(3) Cả 2 nghiệm của phương trình đều nhỏ hơn 1
(4) Phương trình trên có tổng 2 nghiệm là: - log 5 3 7
Số phát biểu đúng là:
A. 1
B. 2
C. 3
D. 4
Tổng các nghiệm của phương trình ( x 2 – 3 ) 2 = 4 ( x – 1 ) 2 là:
A. 10 3
B. 0
C. 1 2
D. 5 3
Tổng các nghiệm của phương trình log 3 ( 2 x + 1 ) - log 1 3 ( 3 - x ) = 0 là:
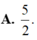

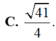
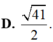
Tìm tổng bình phương các nghiệm của phương trình \(\left(x-1\right)\left(x-3\right)+3\sqrt{x^2-4x+5}-2=0\)
\(\Leftrightarrow x^2-4x+5+3\sqrt{x^2-4x+5}-2=0\)
Đặt \(\sqrt{x^2-4x+5}=t>0\)
\(\Rightarrow t^2+3t-2=0\Rightarrow\left[{}\begin{matrix}t=\dfrac{-3+\sqrt{17}}{2}\\t=\dfrac{-3-\sqrt{17}}{2}\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow x^2-4x+5=\dfrac{13-3\sqrt{17}}{2}\)
\(\Leftrightarrow x^2-4x+\dfrac{-3+3\sqrt{17}}{2}=0\)
\(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=4^2-2\left(\dfrac{-3+3\sqrt{17}}{2}\right)=19-3\sqrt{17}\)
Tổng bình phương các nghiệm của phương trình \(x^3+1=2\sqrt[3]{x^2+5x-2}-2\) trên tập số thực bằng
Em kiểm tra lại đề bài, pt này chắc chắn là ko giải được