Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):2x+2y+z+6=0. Tìm tọa độ điểm M thuộc tia Oz sao cho khoảng cách từ M đến (P) bằng 3.
A . M ( 0 ; 0 ; 21 )
B . M ( 0 ; 0 ; 3 )
C . M ( 0 ; 0 ; 3 ) , M ( 0 ; 0 ; - 15 )
D . M ( 0 ; 0 ; - 15 )
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : 2 x + 2 y + z + 6 = 0 . Tìm tọa độ điểm M thuộc tia Oz sao cho khoảng cách từ M đến (P) bằng 3.
A. M(0;0;21)
B. M(0;0;3)
C. M(0;0;3), M(0;0;-15)
D. M(0;0;-15)
Đáp án B.
Vì M thuộc tia Oz nên:
Vì khoảng cách từ M đến mặt phẳng (P) bằng 3 nên ta có:
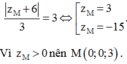
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):2x+2y+z+6=0.Tìm tọa độ điểm M thuộc tia Oz sao cho khoảng cách từ M đến (P) bằng 3.
A. M(0;0;3)
B. M(0;0;3), M(0;0;-15)
C. M(0;0;-15)
D. M(0;0;21)
Tìm một vectơ pháp tuyến của mặt phẳng (P) chứa A 0 ; - 1 ; 1 và B 1 ; 2 ; 0 sao cho 2 điểm E - 1 ; 2 ; 4 và F 3 ; 0 ; - 2 thuộc về hai phía của (P) và khoảng cách từ E tới mặt phẳng (P) bằng khoảng cách từ F tới mặt phẳng (P).
Trong không gian Oxyz, tìm những điểm M trên trục Ox sao cho khoảng cách từ M đến mặt phẳng (P): x - 2y - 2z + 1 = 0 bằng 2
A. M(5;0;0) hoặc M(-7;0;0)
B. M(17;0;0) hoặc M(-19;0;0)
C. M(5;0;0)
D. M(17;0;0)
Trong không gian với hệ tọa độ Oxyz , mặt phẳng α đi qua điểm M(1 ;2 ;1) và cắt tia Ox, Oy, Oz lần lượt tại A, B, C sao cho độ dài OA, OB, OC theo thứ tự tạo thành cấp số nhân có công bội bằng 3. Tính khoảng cách từ gốc tọa độ O tới mặt phẳng α .
A. 4 21
B. 3 21 7
C. 16 91 91
D. 9 21
Trong không gian Oxyz, tìm những điểm M trên tia Oy sao cho khoảng cách từ điểm M đến mặt phẳng (P): x + 2y - 2z + 1 = 0 bằng 3
A. M(0;13;0)
B. M(0;-5;0)
C. M(0;4;0) hoặc M(0;-5;0)
D. M(0;4;0)
Cho đường thẳng đi qua 2 điểm A( 3; -1) ; B( 0;3) ,tìm tọa độ điểm M thuộc Ox sao cho khoảng cách từ M tới đường thẳng AB bằng 1 .
A. (1; 0) và (3; 0)
B.(4; 0)
C. (2; 0)
D.Đáp án khác
Đáp án D
Đường thẳng đi qua 2 điểm A và B có vectơ chỉ phương là 
suy ra tọa độ vectơ pháp tuyến là ( 4;3) .
Suy ra phương trình AB: 4( x-3) + 3( y+ 1) = 0 hay 4x+ 3y -9=0
Do M nằm trên Ox nên M( x; 0)
Do d(M; AB)=1 nên
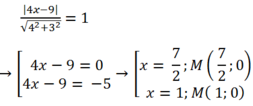
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : 2 x - y + 2 z - 14 = 0 và mặt cầu S : x 2 + y 2 + z 2 - 2 x + 4 y + 2 z - 3 = 0 . Tìm điểm M thuộc (S) sao cho khoảng cách từ M tới (P) lớn nhất.
A. M=(-1;-1''-3)
B. M=(1;-1;-3)
C. M=(-1;1;-3)
D. M=(-1;-1;3)
Chọn A.
Phương pháp: Điểm M là một trong hai giao điểm của đường thẳng (đi qua tâm mặt cầu và vuông góc với mặt phẳng) với mặt cầu.
Cách giải: Phương trình đường thẳng d đi qua tâm mặt cầu vuông góc với mặt phẳng (P) là:
Vậy M = (-1;-1;-3)
