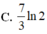Giả sử 1 - x + x 2 n = a 0 + a 1 x + a 2 x 2 + . . . + a 2 n x 2 n . Đặt S = a 0 + a 2 + a 4 + . . . + a 2 n , khi đó S bằng
A. 3 n + 1 2
B. 3 n 2
C. 3 n - 1 2
D. 2 n + 1
Giả sử phương trình Ax2+Bx+C=0 có hai nghiệm x1, x2 thì x + x=-B/A, x*x=C/A. Cho a khác 0 và giả sử phương trình x2 - ax - 1/2a2. Chứng minh rằng x14+x24 >=2+√2
đoạn sau là x2-ax-1/(2a2)=0 nha, viết thiếu.
@nguyenthanhtuan cái này là chứng minh mà bạn.
giả sử x^2+x+1=0 vẫn đúng (vẫn có x thỏa mãn) , tính x^n+1/x^n?
53+12+23-12-32+2=????
Giả sử: (2-x-1)
thì sau khi tính sẽ ra (1-x) hay là (x-1)?
c7:Cho biêu thức A=x+2 phần y-1 và B 4x(x+5) phần y+2
a) giả sử biết y=2 giải pt ẩn x A+3=B
b) Giả sử đẫ biết x=-3 giải pt ẩn y A-B =13
Giả sử a * b = 3a - b. Hỏi x bằng bao nhiêu nếu: 2 * (5 * x ) = 1?
Ta có 2*(5*x) = 1
<=> 3.2 - (5*x) = 1
<=> 6 - (3.5 - x) = 1
<=> 6 - (15-x) = 1
<=> 6 - 15 + x = 1
<=> (-9) + x = 1
<=> x = 10
Giả sử f(x) chia x+1 dư 5 khi chia cho x-2 dư 7. Hỏi khi chia f(x) cho (x+1)(x-2) thì dư bao nhiêu?
Từ giả thiết ta có thể viết \(f\left(x\right)=g\left(x\right)\left(x+1\right)+5\) (1)
Và \(f\left(x\right)=h\left(x\right)\left(x-2\right)+7\) (2)
Do (x + 1)(x - 2) là đa thức bậc 2 nên số dư là đa thức bậc 1. Tức là:
\(f\left(x\right)=\left(x+1\right)\left(x-2\right)t\left(x\right)+ax+b\) (Với g(x) , h(x), t(x) là các đa thức)
Ta có \(f\left(x\right)=\left(x+1\right)\left(x-2\right)t\left(x\right)+a\left(x+1\right)+b-a=\left(x+1\right)\left[\left(x-2\right)t\left(x\right)+a\right]+b-a\)
Theo (1) thì b - a = 5.
Ta cũng có :
\(f\left(x\right)=\left(x+1\right)\left(x-2\right)t\left(x\right)+a\left(x-2\right)+b+2a=\left(x-2\right)\left[\left(x+1\right)t\left(x\right)+a\right]+b+2a\)
Theo (2) thì b + 2a = 7.
Từ đó ta tìm được \(a=\frac{2}{3};b=\frac{17}{3}\)
giả sử x,y>0 x,y thuộc R thỏa (cănx+1).(căny+1)>=4
tìm GTNN của P=x^2/y + y^2/x
c7: Cho hai biểu thức A=x+2 phần y-1 và B=4x(x+5) phần y+2
a) Giả sử đã biêt y=2 hãy giải pt ẩn x A+3 =B
b) Giả sử đã biêt x=-3 hãy giải pt ẩn y A-B =13
a: y=2 thì \(A=\dfrac{x+2}{2-1}=x+2\)
\(B=\dfrac{4x\left(x+5\right)}{2+2}=x\left(x+5\right)\)
A+3=B
=>x+5=x(x+5)
=>(x+5)(1-x)=0
=>x=1 hoặc x=-5
b: Khi x=-3 thì \(A=\dfrac{-3+2}{y-1}=\dfrac{-1}{y-1}\)
\(B=\dfrac{4\cdot\left(-3\right)\cdot\left(-3+5\right)}{y+2}=\dfrac{-12\cdot2}{y+2}=\dfrac{-24}{y+2}\)
A-B=13
\(\Leftrightarrow-\dfrac{1}{y-1}+\dfrac{24}{y+2}=13\)
\(\Leftrightarrow13\left(y-1\right)\left(y+2\right)=-y-2+24y-24\)
\(\Leftrightarrow13y^2+13y-26=23y-26\)
=>y(13y-10)=0
=>y=0 hoặc y=10/13
Giả sử x và y là hai số thỏa mãn x> y và xy = 1. Tìm GTNN của biểu thức: A=\(\dfrac{x^2+y^2}{x-y}\)
Giả sử F(x) là một nguyên hàm của f ( x ) = ln ( x + 3 ) x 2 sao cho F(-2)+F(1)=0. Giá trị của F(-1)+F(2) bằng
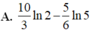
B. 0