Trong không gian Oxyz, tìm tất cả các giá trị của tham số m để  x 2 + y 2 + z 2 + 2 x - 4 y + 4 z + m = 0 là phương trình mặt cầu.

A.  m > 9

B.  m ≤ 9

C.  m < 9

D.  m ≥ 9

Trong không gian với hệ trục tọa độ Oxyz , cho đường thẳng d có phương trình x = 6 + t y = - 2 - 5 t z = - 1 + t . Xét đường thẳng ∆ : x - a 5 = y - 1 - 12 = z + 5 - 1 , với a là tham số thực. Tìm tất cả các giá trị của a để đường thẳng d và ∆ cắt nhau.

A. a = 0

B. a = 4

C. a = 8

D.  a = 1 2

Trong không gian với hệ tọa độ Oxyz, tìm tất cả các giá trị của tham số m để phương trình x 2 + y 2 + z 2 - 4 x + 2 m y + 6 z + 13 = 0  là phương trình của mặt cầu.

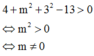
Trong không gian với hệ tọa độ Oxyz, tìm tất cả các giá trị của tham số m để phương trình  x 2 + y 2 + z 2 - 4 x + 2 m y + 6 z + 13 = 0 là phương trình của mặt cầu.

A .   m > 0  

B .   m ≠ 0

C .   m ∈ R

D .   m > 0

Trong không gian Oxyz, cho phương trình x 2 + y 2 + z 2 - 2 ( m + 2 ) x + 4 m y - 2 m z + 5 m 2 + 9 = 0 . Tìm tất cả các giá trị của m để phương trình trên là phương trình của một mặt cầu

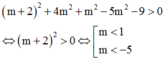
Trong không gian Oxyz, cho mặt cầu (S): ( x - 2 ) 2 + ( y + 1 ) 2 + ( z + 2 ) 2 = 4  và mặt phẳng (P): 4x-3y-m=0. Tìm tất cả các giá trị thực của tham số m để mặt phẳng (P) và mặt cầu (S) có đúng 1 điểm chung

A. m=1

B. m=-1 hoặc m=-21

C. m=1 hoặc m=21

D. m=-9 hoặc m=31

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): ( x + 3 ) 2 + y 2 + ( z - 2 ) 2 = m 2 + 4 . Tìm tất cả các giá trị thực của tham số m để mặt cầu (S) tiếp xúc với mặt phẳng (Oyz).

Trong không gian với hệ toạ độ Oxyz, cho đường thẳng Δ : x - 1 1 = y + 2 2 = z + 1 - 1 và mặt phẳng ( α ) :mx+10y-5z+1=0. Tìm tất cả các giá trị của tham số m để Δ ⊥ ( α ) .

A. m=-25.

B. m=5.

C. m=25.

D. m=-5.

Trong không gian với hệ trục tọa độ Oxyz, có tất cả bao nhiêu số tự nhiên của tham số m để phương phương trình  x 2 + y 2 + z 2 + 2 ( m - 2 ) y - 2 ( m + 3 ) z + 3 m 2 + 7 = 0  là phương trình của một mặt cầu.

A. 2

B. 3

C. 4

D. 5