Giả sử a,b là các số thực sao cho x 3 + y 3 = a . 10 3 x + b . 10 2 x đúng với mọi số thực dương x,y,z thỏa mãn log(x+y)=z và log x 2 + y 2 = z + 1 Giá trị của a+b bằng:
A. -31/2
B. -25/2
C. 31/2
D. 29/2
Bài tập số 2:
Giả sử x và y là các biến
số. Hãy cho biết kết quả của việc thực hiện thuật toán sau:
Bước 1: x ← x + y
Bước 2: y ← x – y
Bước 3: x ← x – y
Bài tập số 3: Cho trước 3 số dương a,b và c. Hãy mô tả thuật toán cho biết ba số đó có thể là độ
dài ba cạnh của một tam giác hay không?
Bài tập số 4:
Cho 2 biến x và y. Hãy
mô tả thuật toán đổi giá trị của các biến nói trên (nếu cần) để x và y theo thứ
tự có giá trị không giảm.
Bài tập số 5:
Hãy cho biết kết quả của
thuật toán sau:
Bước 1: SUM ← 0; i ← 0.
Bước 2: Nếu i>100 thì chuyển tới bước 4.
Bước 3: i ← i + 1; SUM ← SUM + i. Quay lại bước 2;
Bước 4: Thông báo giá trị của SUM và kết thúc thuật toán.
Bài tập 1:
a. Xác định số học sinh trong lớp cùng mang họ Trần?
b. Tính tổng của các phần tử lớn hơn 0 trong dãy n số cho trước?
c. Tìm số các số có giá trị nhỏ nhất trong n số đã cho?
Bài làm
a. Input: danh sách học sinh trong lớp
Output: ds học sinh cùng mang họ Trần.
b. Input: dãy n số
Output: tổng các phần tử lớn hơn 0.
c. Input: n số đã cho
Output: số các số có giá trị nhỏ nhất.
Giả sử a,b là các số thực sao cho x 3 + y 3 = a 10 3 x + b 10 2 x đúng với mọi các số thực dương x, y, z thỏa mãn log ( x + y ) = z và log ( x 2 + y 2 ) = z + 1 . Giá trị của a+b bằng
A. -31/2
B. -25/2
C. 31/2
D. 29/2
Giả sử a, b là các số thực sao cho x 3 + y 3 = a .10 3 z + b .10 2 z đúng với mọi các số thực dương x, y, z thỏa mãn log x + y = z v à log x 2 + y 2 = z + 1 . Giá trị của a + b bằng
A. − 29 2 .
B. 31 2 .
C. - 31 2 .
D. 29 2 .
Giả sử a, b là các số thực sao cho x 3 + y 3 = a .10 3 z + b .10 2 z đúng với mọi các số thực dương x, y, z thỏa mãn log x + y = z và log x 2 + y 2 = z + 1 . Giá trị của a + b bằng
A. - 31 2
B. - 25 2
C. 31 2
D. 29 2
Giả sử a, b là các số thực sao cho x 3 + y 3 = a . 10 3 z + b . 10 2 z đúng với mọi các số thực dương x, y, z thỏa mãn
log x + y = z và log x 2 + y 2 = z + 1 . Giá trị của a+b bằng
A. - 31 2
B. - 25 2
C. 31 2
D. 29 2
Giả sử a, b là các số thực sao cho x3 + y3 = a.103x + b.102x đúng với mọi số thực dương x, y, z thỏa mãn log (x + y) = z và log(x2 + y2) = z + 1. Giá trị của a+b bằng:
A. - 31 2
B. - 25 2
C. 31 2
D. 29 2
Đáp án D.
Ta có
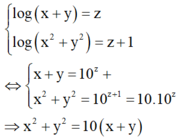
Khi đó
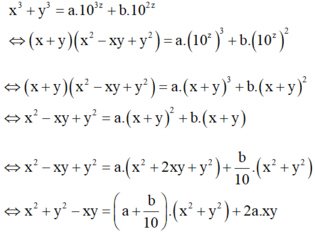
Đồng nhất hệ số, ta được

Giả sử a, b là các số thực sao cho x 3 + y 3 = a .10 3 x + b .10 2 x đúng với mọi số thực dương x, y, z thỏa mãn log x + y = z và log x 2 + y 2 = z + 1. Giá trị của a+b bằng:
A. − 31 2 .
B. − 25 2 .
C. 31 2 .
D. 29 2 .
Đáp án D.
Ta có:
log x + y = z log x 2 + y 2 = z + 1 ⇔ x + y = 10 z + x 2 + y 2 = 10 z + 1 = 10.10 z ⇒ x 2 + y 2 = 10 x + y
Khi đó:
x 3 + y 3 = a .10 3 z + b .10 2 z ⇔ x + y x 2 − x y + y 2 = a . 10 z 3 + b . 10 z 2 ⇔ x + y x 2 − x y + y 2 = a . x + y 3 + b . x + y 2 ⇔ x 2 − x y + y 2 = a . x + y 2 + b . x + y ⇔ x 2 − x y + y 2 = a . x 2 + 2 x y + y 2 + b 10 . x 2 + y 2 ⇔ x 2 + y 2 − x y = a + b 10 . x 2 + y 2 + 2 a . x y
Đồng nhất hệ số, ta được:
a + b 10 = 1 2 a = − 1 ⇒ a = − 1 2 b = 15 .
Vậy a + b = 29 2 .
Giả sử x, y là các biến nguyên (kiểu integer), z là biến kiểu real (thực), a là biến kiểu Char (kiểu kí tự), các câu lệnh nào sau đây không phù hợp? vì sao? x := 3; y:= x; z := 3.3; x := z; Y := 6.8; a:= ‘z’; a:=x; x:=a; y:= ‘z’; y := y + 1; x := y*3 + 2; y – 1 := x; x*y := x+1;
Giả sử x, y là các biến nguyên (kiểu integer), z là biến kiểu real (thực), a là biến kiểu Char (kiểu kí tự), các câu lệnh nào sau đây không phù hợp? vì sao? x := 3; y:= x; z := 3.3; x := z; Y := 6.8; a:= ‘z’; a:=x; x:=a; y:= ‘z’; y := y + 1; x := y*3 + 2; y – 1 := x; x*y := x+1; Giúp mình với :((