Cho phương trình e m . cos x - sin x - e 2 1 - sin x = 2 - sin x - m . cos x với m là tham số thực. Gọi S là tập hợp tất cả các giá trị của m để phương trình có nghiệm. Khi đó S=( - ∞ ; a ] ∪ [ b ; + ∞ ). Tính T=10a+20b
A. 10 3
B . 0
C. 19
D. -1
Những câu hỏi liên quan
Số giá trị nguyên của m để phương trình \(2\sin^2x-\sin x\cos x-m\cos^2x=1\) có nghiệm trên
Cho phương trình
cos
x
+
sin
x
1
+
sin
2
x
+
cos
2
x
. Nghiệm của phương trình có dạng
x
1
a
π
+
k
π
.
x
2
±
b
π
+
k
2
π
b
0
Tính tổng a + b A. ...
Đọc tiếp
Cho phương trình cos x + sin x = 1 + sin 2 x + cos 2 x . Nghiệm của phương trình có dạng x 1 = a π + k π . x 2 = ± b π + k 2 π b > 0 Tính tổng a + b
A. 1 12
B. 3
C. 7 π 12
D. π 4
Có bao nhiêu giá trị nguyên của tham số m để phương trình
sin
2
x
+
cos
2
x
+
|
sin
x
+
cos
x
|
-
cos
2
x
+
m
-
m
0
có nghiệm thực? A. 9 B. 2 C. 3 D. 5
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để phương trình sin 2 x + cos 2 x + | sin x + cos x | - cos 2 x + m - m = 0 có nghiệm thực?
A. 9
B. 2
C. 3
D. 5
Đáp án C
Sử dụng tính đơn điệu của hàm số, đánh giá số nghiệm của phương trình.
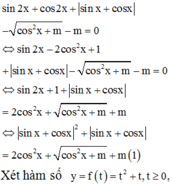
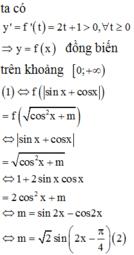
Vậy, có 3 giá trị nguyên của m thỏa mãn yêu cầu đề bài.
Đúng 0
Bình luận (0)
Cho phương trình:
cos
2
x
+
sin
x
-
1
0
*
. Bằng cách đặt
t
sin
x
-
1
≤
x
≤
1
thì phương trình (*) trở thành phương trình nào sau đây A.
-
2
t...
Đọc tiếp
Cho phương trình: cos 2 x + sin x - 1 = 0 * . Bằng cách đặt t = sin x - 1 ≤ x ≤ 1 thì phương trình (*) trở thành phương trình nào sau đây
A. - 2 t 2 + t = 0
B. t 2 + t + 2 = 0
C. - 2 t 2 + t - 2 = 0
D. - t 2 + t = 0
Cho phương trình m. sin x + 4. cos x = 2m - 5 với m là tham số. Có bao nhiêu giá trị nguyên của m để phương trình có nghiệm?
A. 4
B. 7.
C. 6.
D. 5
Số nghiệm của phương trình
sin
x
.
sin
2
x
+
2
.
sin
x
.
cos
2...
Đọc tiếp
Số nghiệm của phương trình sin x . sin 2 x + 2 . sin x . cos 2 x + sin x + cos x sin x + cos x = 3 . cos 2 x trong khoảng - π , π là:
A. 2
B. 4
C. 3
D. 5
Trong các phương trình sau:
cos
x
5
-
3
(1);
sin
x
1
-
2
(2);
sin
x
+
cos
x
2
(3), phương trình nào vô nghiệm? A. (2) B. (1) C. (3) D. (1) và (2)
Đọc tiếp
Trong các phương trình sau: cos x = 5 - 3 (1); sin x = 1 - 2 (2); sin x + cos x = 2 (3), phương trình nào vô nghiệm?
A. (2)
B. (1)
C. (3)
D. (1) và (2)
Trong các phương trình sau: cos x = 5 - 3 (1); sin x = 1 - 2 (2); sin x + cos x = 2 (3), phương trình nào vô nghiệm?
A. (2).
B. (1).
C. (3).
D. (1) và (2).
Chọn C
Ta có: 
nên (1) và (2) có nghiệm.
Cách 1:
Xét: 
nên (3) vô nghiệm.
Cách 2:
Điều kiện có nghiệm của phương trình: sin x + cos x = 2 là: 
(vô lý) nên (3) vô nghiệm.
Cách 3:
Vì 
nên (3) vô nghiệm.
Đúng 0
Bình luận (0)
Giải phương trình
cos
x
+
cos
3
x
sin
x
-
sin
3
x
.
A
.
x
-
π
4
+
k
π
2
k
∈
ℤ
B
.
x...
Đọc tiếp
Giải phương trình cos x + cos 3 x = sin x - sin 3 x .
A . x = - π 4 + k π 2 k ∈ ℤ
B . x = π 4 + k π 2 k ∈ ℤ
C . x = π 4 + k π k ∈ ℤ
D . x = π 4 + k 2 π k ∈ ℤ
câu này nhìn ngứa mắt quá làm kiểu gì giờ ???
12 tháng 7 2021 lúc 21:44
Giải các Phương trình sau
a) \(sin^4\frac{x}{2}+cos^4\frac{x}{2}=\frac{1}{2}\)
b) \(sin^6x+cos^6x=\frac{7}{16}\)
c) \(sin^6x+cos^6x=cos^22x+\frac{1}{4}\)
d) \(tanx=1-cos2x\)
e) \(tan(2x+\frac\pi3).tan(\frac\pi3-x)=1\)
f) \(tan(x-15^o).cot(x+15^o)=\frac{1}{3}\)
a.
\(\left(sin^2\dfrac{x}{2}+cos^2\dfrac{x}{2}\right)^2-2sin^2\dfrac{x}{2}cos^2\dfrac{x}{2}=\dfrac{1}{2}\)
\(\Leftrightarrow2-\left(2sin\dfrac{x}{2}cos\dfrac{x}{2}\right)^2=1\)
\(\Leftrightarrow1-sin^2x=0\)
\(\Leftrightarrow cos^2x=0\)
\(\Leftrightarrow x=\dfrac{\pi}{2}+k\pi\)
Đúng 2
Bình luận (0)
b.
\(\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)=\dfrac{7}{16}\)
\(\Leftrightarrow1-\dfrac{3}{4}\left(2sinx.cosx\right)^2=\dfrac{7}{16}\)
\(\Leftrightarrow16-12.sin^22x=7\)
\(\Leftrightarrow3-4sin^22x=0\)
\(\Leftrightarrow3-2\left(1-cos4x\right)=0\)
\(\Leftrightarrow cos4x=-\dfrac{1}{2}\)
\(\Leftrightarrow4x=\pm\dfrac{2\pi}{3}+k2\pi\)
\(\Leftrightarrow x=\pm\dfrac{\pi}{6}+\dfrac{k\pi}{2}\)
Đúng 1
Bình luận (0)
c.
\(\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)=cos^22x+\dfrac{1}{4}\)
\(\Leftrightarrow1-\dfrac{3}{4}\left(2sinx.cosx\right)^2=cos^22x+\dfrac{1}{4}\)
\(\Leftrightarrow3-3sin^22x=4cos^22x\)
\(\Leftrightarrow3=3\left(sin^22x+cos^22x\right)+cos^22x\)
\(\Leftrightarrow3=3+cos^22x\)
\(\Leftrightarrow cos2x=0\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời