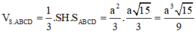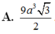
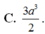
Cho hình chóp S . A B C D có đáy A B C D là hình vuông cạnh a . Mặt bên S A B là tam giác đều nằm trong mặt phẳng vuông góc với đáy A B C D .Thể tích khối chóp S . A B C D là:
A. a 3 3 6
B. a 3 3 4
C. a 3 3 2
D. a 3 3
Đáp án là A
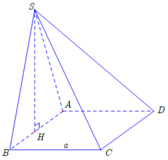
Gọi H là trung điểm A B .
Ta có S A B ⊥ A B C D S A B ∩ A B C D = A B S H ⊂ S A B ; S H ⊥ A B ⇒ S H ⊥ A B C D .
Khi đó: V S . A B C D = 1 3 S H . S A B C D = 1 3 . a 3 2 . a 2 = a 3 3 6 .
Cho hình vuông S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt bên SAB là tam giác vuông tại S và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối cầu ngoại tiếp hình chóp S.ABCD là:
A. 2 π a 3 3
B. 2 π a 3 6
C. 2 π a 3
D. 2 π a 3 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (ABCD). Biết thể tích khối chóp S.ABCD bằng a 3 3 6 . Độ dài cạnh bên SA bằng bao nhiêu?
A. S A = a .
B. S A = a 2 .
C. S A = a 3 2 .
D. S A = a 3 .
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (ABCD). Biết thể tích khối chóp S.ABCD bằng a 3 6 .
Độ dài cạnh bên SA bằng bao nhiêu?
A. SA = a
B. SA = a 2
C. SA = a 3 2
D. SA = a 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (ABCD). Biết thể tích khối chóp S.ABCD bằng a 3 3 6 . Độ dài cạnh bên SA bằng bao nhiêu?
A. SA = a
B. S A = a 2
C. S A = a 3 2 .
D. S A = a 3 .
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (ABCD). Biết thể tích khối chóp S.ABCD bằng a 3 3 6 . Độ dài cạnh bên SA bằng bao nhiêu?
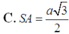
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng đáy bằng Thể tích khối chóp S.ABCD bằng
A. a 3 3 12
B. a 3 3 9
C. a 3 5 24
D. a 3 5 6
Chọn đáp án D
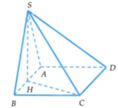
Gọi H là trung điểm của AB. Từ giả thiết ta có S H ⊥ A B C D
Suy ra 
⇒ S H C vuông cân tại H.
Do ∆ B H C vuông tại H nên
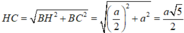
⇒ S H = H C = a 5 2
Thể tích khối chóp V S . A B C D = 1 3 S H . S A B C D = a 3 5 6 đ v t t là
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy, góc giữa đường thẳng SC và mặt phẳng đáy bằng 45 o . Thể tích khối chóp S.ABCD bằng:
A. a 3 3 12
B. a 3 3 9
C. a 3 5 24
D. a 3 5 6
Chọn D
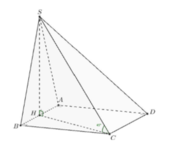
Gọi H là trung điểm của AB.
Do đó:
Xét tam giác vuông BHC:
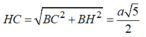
Xét tam giác vuông SHC:
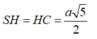
Suy ra:
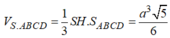
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy, góc giữa đường thẳng SC và mặt phẳng đáy bằng 45 ° . Thể tích khối chóp S.ABCD bằng:
A. a 3 3 12
B. a 3 3 9
C. a 3 5 24
D. a 3 5 6
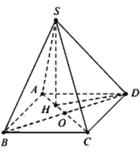
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu của S lên mặt phẳng đáy trùng với trọng tâm tam giác ABD. Cạnh bên SD tạo với đáy một góc 60 0
Tính thể tích khối chóp S.ABCD
A. a 3 15 3
B. a 3 15 27
C. a 3 15 9
D. a 3 3
Đáp án C
Phương pháp giải:
Xác định hình chiếu của đỉnh, xác định góc để tìm chiều cao và áp dụng công thức thể tích
Lời giải:
Gọi O là tâm hình vuông ABCD , H là trọng tâm tam giác ABD
Ta có 
ABCD là hình vuông cạnh a nên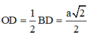 
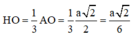
Tam giác HDO vuông tại O, có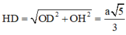 
Tam giác SHD vuông tại H, có 
Vậy thể tích cần tính là 
