Cho hình phẳng (H) giới hạn bởi đường cong (C) y = x 3 - 3 x + 2 và (P) y = 2 x + 2 . Thể tích của khối tròn xoay nhận được khi cho (H) quay quanh trục Ox có dạng V = πa b + 2018 c + 2019 d Hỏi mệnh đề nào trong các mệnh đề sau là sai?
![]()
![]()
![]()
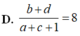
Cho hình phẳng (H) giới hạn bởi đường cong có phương trình y = x 2 - 4 x + 3 và đường thẳng y = x + 3 (phần đô đậm trong hình vẽ). Tính diện tích S của hình phẳng (H).
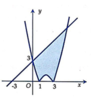
A. S = 47 2
B. S = 39 2
C. S = 169 6
D. S = 109 6
Cho hình phẳng (H) giới hạn bởi đường cong có phương trình
y
=
x
2
−
4
x
+
3
và đường thẳng y=x+3 (phần đô đậm trong hình vẽ). Tính diện tích S của hình phẳng (H)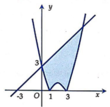
A. S = 47 2 .
B. S = 39 2 .
C. S = 169 2 .
D. S = 109 2 .
Cho hình phẳng (H) giới hạn bởi đường cong có phương trình y = x 2 - 4 x + 3 và đường thẳng y = x + 3 (phần đô đậm trong hình vẽ). Tính diện tích S của hình phẳng
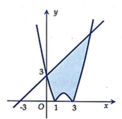
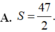
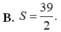
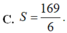
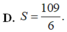
Lời giải:
Trước tiên ta tìm giao điểm của 2 ĐTHS:
PT hoành độ giao điểm: $|x^2-4x+3|=x+3$
$\Rightarrow x=0$ hoặc $x=5$
Diện tích hình phẳng giới hạn bởi $(C)$ và $(d)$ là:
\(\int ^5_0(x+3-|x^2-4x+3|)dx=\frac{109}{6}\) (đơn vị diện tích)
Diện tích hình phẳng giới hạn bởi đường thẳng y=x+3 , đường cong y=x^2+1 là
Phương trình hoành độ giao điểm:
\(x^2+1=x+3\Leftrightarrow x^2-x-2=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=2\end{matrix}\right.\)
\(S=\int\limits^2_{-1}\left|x^2-x-2\right|dx=\int\limits^2_{-1}\left(-x^2+x+2\right)dx=\left(-\dfrac{1}{3}x^3+\dfrac{1}{2}x^2+2x\right)|^2_{-1}=\dfrac{9}{2}\)
Cho (H) là hình phẳng giới hạn bởi đường cong y = x , trục hoành và đường thẳng y=2-x (phần tô đậm trong hình vẽ bên). Diện tích của (H) bằng
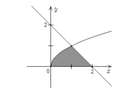
A. 4 2 - 1 3
B. 7 6
C. 8 2 + 3 6
D. 5 6
Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x), y=0, x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0, x=a bằng:
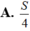
![]()
![]()
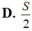
Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x),y=0,x=0,x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0,x=a bằng
A. S/4.
B. 4S.
C. 2S.
D. S/2.
a. Tính S hình phẳng giới hạn bởi đồ thị y = ex(1+x)/1+xex , trục tung và trục hoành.
b. Tính S hình phẳng giới hạn bởi đồ thị hàm số y =3x , trục Oy và đường thẳng x=2.
c. tính S hình phẳng giới hạn bởi hàm số y = x4-4x2+4, y=x2 , trục tung và đường thẳng x=1.
d. Tính S hình phẳng giới hạn bởi hình cong (C) y= 2x+1/x+1 , tiệm cận ngang của (C) và 2 đường thẳng x=1, x=3
e. Tính S hình phẳng giới hạn bởi hàm số y = 2-x2 vvà y=x và các đường thẳng x=-2 , x=1
a. Pt hoành độ giao điểm: \(\frac{e^x\left(1+x\right)}{1+xe^x}=0\Rightarrow x=-1\)
Diện tích:
\(S=\int\limits^0_{-1}\frac{e^x+xe^x}{1+xe^x}dx\)
Đặt \(1+xe^x=t\Rightarrow\left(e^x+xe^x\right)dx=dt\) ; \(\left\{{}\begin{matrix}x=-1\Rightarrow t=1-\frac{1}{e}\\x=0\Rightarrow t=1\end{matrix}\right.\)
\(S=\int\limits^1_{1-\frac{1}{e}}\frac{dt}{t}=ln\left|t\right||^1_{1-\frac{1}{e}}=-ln\left|\frac{e-1}{e}\right|=ln\left(\frac{e}{e-1}\right)\)
b. Đồ thị \(y=3^x\) ko cắt trục hoành
Diện tích:
\(S=\int\limits^2_03^xdx=\frac{3^x}{ln3}|^2_0=\frac{9}{ln3}-\frac{1}{ln3}=\frac{8}{ln3}\)
c.
Pt hoành độ giao điểm:
\(x^4-4x^2+4=x^2\Leftrightarrow x^4-5x^2+4=0\Rightarrow\left[{}\begin{matrix}x^2=1\\x^2=4\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
Diện tích:
\(S=\int\limits^1_0\left(x^4-4x^2+4-x^2\right)dx=\int\limits^1_0\left(x^4-5x^2+4\right)dx\)
\(=\left(\frac{1}{5}x^5-\frac{5}{3}x^3+4x\right)|^1_0=\frac{38}{15}\)
d.
\(\lim\limits_{x\rightarrow\infty}\frac{2x+1}{x+1}=2\Rightarrow y=2\) là TCN của (C)
Diện tích:
\(S=\int\limits^3_1\left(2-\frac{2x+1}{x+1}\right)dx=\int\limits^3_1\frac{1}{x+1}dx=ln\left|x+1\right||^3_1=ln4-ln2=ln2\)
e.
Pt hoành độ giao điểm:
\(2-x^2=x\Leftrightarrow x^2+x-2=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
Diện tích:
\(S=\int\limits^1_{-2}\left(2-x^2-x\right)dx=\left(2x-\frac{1}{3}x^3-\frac{1}{2}x^2\right)|^1_{-2}=\frac{9}{2}\)
Tính diện tích hình phẳng giới hạn bởi đường cong y = x 2 - x + 3 và đường thẳng y=2x+1
A. 1/3
B. 1/6
C. 1/4
D. 1/2