Các câu hỏi tương tự
Diện tích hình phẳng giới hạn bởi parabol
y
x
-
2
2
, đường cong
y
x
3
và trục hoành bằng (phần tô đậm trong hình vẽ bên) A.
11
2
B.
73
12
C.
7...
Đọc tiếp
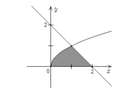
Diện tích hình phẳng giới hạn bởi parabol y = x - 2 2 , đường cong y = x 3 và trục hoành bằng (phần tô đậm trong hình vẽ bên)
A. 11 2
B. 73 12
C. 7 12
D. 5 2
Cho (H) là hình phẳng giới hạn bởi parabol
y
1
4
x
2
+
1
với
0
≤
x
≤
2
2
, nửa đường tròn
y
8
-
x...
Đọc tiếp
Cho (H) là hình phẳng giới hạn bởi parabol y = 1 4 x 2 + 1 với 0 ≤ x ≤ 2 2 , nửa đường tròn y = 8 - x 2 và trục hoành, trục tung (phần tô đậm trong hình vẽ). Diện tích của (H) bằng
A. 3 π + 14 6
B. 3 π + 2 3
C. 3 π + 4 3
D. c
Cho (H) là hình phẳng giới hạn bởi parabol
y
1
4
x
2
+
1
(với
0
≤
x
≤
2
2
), nửa đường tròn
y
8
-
x
2
và trục hoành, trục tung (phần tô đậm trong hình vẽ). Diện tích của (H) bằng A. ...
Đọc tiếp
Cho (H) là hình phẳng giới hạn bởi parabol y = 1 4 x 2 + 1 (với 0 ≤ x ≤ 2 2 ), nửa đường tròn y = 8 - x 2 và trục hoành, trục tung (phần tô đậm trong hình vẽ). Diện tích của (H) bằng
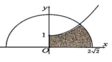
A. 3 π + 14 6
B. 2 π + 2 3
C. 3 π + 4 6
D. 3 π + 2 3
Cho hình (H) là hình phẳng giới hạn bởi parabol
y
x
2
-
4
x
+
4
, đường cong
y
x
3
và trục hoành (phần tô đậm trong hình vẽ). Tính diện tích S của hình (H) A.
S
11
2
B.
S
7
2
C.
S...
Đọc tiếp
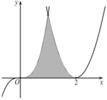
Cho hình (H) là hình phẳng giới hạn bởi parabol y = x 2 - 4 x + 4 , đường cong y = x 3 và trục hoành (phần tô đậm trong hình vẽ). Tính diện tích S của hình (H)
A. S = 11 2
B. S = 7 2
C. S = 20 3
D. S = - 11 2
Cho hình (H) là hình phẳng giới hạn bởi parabol
y
x
2
-
4
x
+
4
đường cong
y
x
3
và trục hoành (phần tô đậm trong hình vẽ). Tính diện tích S của hình (H). A.
S
11
2
B.
S
7
12
C.
S...
Đọc tiếp
Cho hình (H) là hình phẳng giới hạn bởi parabol y = x 2 - 4 x + 4 đường cong y = x 3 và trục hoành (phần tô đậm trong hình vẽ). Tính diện tích S của hình (H).
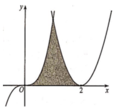
A. S = 11 2
B. S = 7 12
C. S = 20 3
D. S = - 11 2
Cho (H) là hình phẳng giới hạn bởi parabol
y
2
x
2
4
đường cong
y
1
-
x
2
4
(với
0
≤
x
≤
2
) và trục hoành (tham khảo hình vẽ bên).Diện tích của (H) bằng A. ...
Đọc tiếp
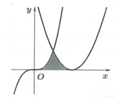
Cho (H) là hình phẳng giới hạn bởi parabol y = 2 x 2 4 đường cong y = 1 - x 2 4 (với 0 ≤ x ≤ 2 ) và trục hoành (tham khảo hình vẽ bên).
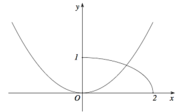
Diện tích của (H) bằng
A. 3 π - 2 12
B. 3 π + 4 2 - 6 12
C. 4 π + 3 2 - 8 12
D. π + 2 - 2 3
Cho (H) là hình phẳng giới hạn bởi Parabol
y
3
x
2
,
cung tròn có phương trình
y
4
−
x
2...
Đọc tiếp
Cho (H) là hình phẳng giới hạn bởi Parabol y = 3 x 2 , cung tròn có phương trình y = 4 − x 2 0 ≤ x ≤ 2 và trục hoành (phần tô đậm trong hình vẽ). Diện tích của (H) bằng:
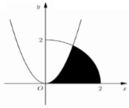
A. 4 π + 3 12 .
B. 4 π − 3 6 .
C. 4 π + 2 3 − 3 6 .
D. 5 3 − 2 π 3 .
Gọi H là hình phẳng giới hạn bởi đồ thị hàm số
y
x
, cung tròn có phương trình
y
6
-
x
2
-
6
≤
x
≤
6
và trục hoành (phần tô đậm trong hình vẽ bên). Tính thể tích V của vật thể tròn xoay sinh bở...
Đọc tiếp
Gọi H là hình phẳng giới hạn bởi đồ thị hàm số y = x , cung tròn có phương trình y = 6 - x 2 - 6 ≤ x ≤ 6 và trục hoành (phần tô đậm trong hình vẽ bên). Tính thể tích V của vật thể tròn xoay sinh bởi khi quay hình phẳng H quanh trục
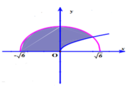
A. V = 4 π 6 + 22 π
B. V = π 6 - 22 π 3
C. V = 8 π 6 + 11 π
D. V = 4 π 6 + 22 π 3
Cho (H) là hình phẳng giới hạn bởi parabol
y
2
x
2
4
, đường cong
1
-
x
2
4
(với
0
≤
x
≤
2
) và trục hoành (tham khảo hình vẽ bên). Diện tích của (H) bằng A.
3...
Đọc tiếp
Cho (H) là hình phẳng giới hạn bởi parabol y = 2 x 2 4 , đường cong 1 - x 2 4 (với 0 ≤ x ≤ 2 ) và trục hoành (tham khảo hình vẽ bên). Diện tích của (H) bằng
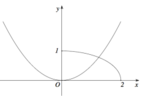
A. 3 π - 2 12
B. 3 π + 4 2 - 6 12
C. 4 π + 3 2 - 8 12
D. π + 2 - 2 3