Trong không gian với hệ tọa độ Oxyz, cho hình thang ABCD có hai đáy AB, CD; có tọa độ ba đỉnh A ( 1 ; 2 ; 1 ) , B ( 2 ; 0 ; - 1 ) , C ( 6 ; 1 ; 0 ) . Biết hình thang có diện tích bằng 6 2 . Giả sử đỉnh D ( a ; b ; c ) , tìm mệnh đề đúng?
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho hình thang cân ABCD có AB là đáy lớn, CD là đáy nhỏ và A ( 3;-1;-2 ); B ( 1;5;1 ); C ( 2;3;3 ). Tìm tọa độ điểm D của hình thang cân.
A. D ( 4;3;0 )
B. D 164 49 ; 51 49 ; 48 49
C. D 1 2 ; 1 3 ; 1 4
D. D ( -4;3;0 )
Vì ABCD là hình thang cân nên AD = BC = 3.
Gọi ∆ là đường thẳng qua C và song song với AB.
Gọi (S) là mặt cầu tâm A bán kính R = 3. Điểm D cần tìm là giao điểm của ∆ và (S).
Đường thẳng ∆ có vectơ chỉ phương A B → - 2 ; 6 ; 3 nên có phương trình:
x = 2 - 2 t y = 3 + 6 t z = 3 + 3 t
Phương trình mặt cầu
S : x - 3 2 + y + 1 2 + z + 2 2 = 9 .
Tọa độ điểm D là nghiệm của phương trình
- 2 t - 1 2 + 6 t + 4 2 + 3 t + 5 2 = 9 ⇔ 49 t 2 + 82 t + 33 = 0 ⇔ t = - 1 t = - 33 49 .
Đáp án B
Trong không gian vói hệ trục tọa độ Oxyz, cho hình thang cân ABCD có hai đáy AB, CD thỏa mãn CD=2AB và diện tích bằng 28, đỉnh A ( - 1 ; - 1 ; 0 ) , phương trình đường thẳng chứa cạnh CD là x - 2 2 = y + 1 2 = z - 3 1 . Tìm tọa độ điểm D biết hoành độ điểm B lớn hơn hoành độ điểm A.
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho các điểm A - 1 ; 0 ; 1 , B 1 ; 1 ; - 1 , C 5 ; 0 ; - 2 . Tìm tọa độ điểm H sao cho tứ giác ABCH là thành hình thang cân với hai đáy AB, CH.
A. H(3;-1;0)
B. H(7;1;-4)
C. H(-1;-3;4)
D. H(1;-2;2)
Chọn C.
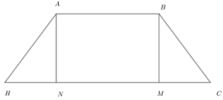
Phương pháp: Sử dụng các véc tơ bằng nhau.

Giả sử M,N lần lượt là hình chiếu của A, B lên CH.
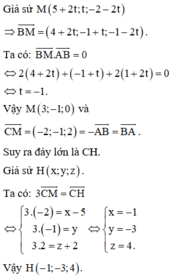
Trong không gian với hệ tọa độ Oxyz, cho các điểm A − 1 ; 0 ; 1 , B 1 ; 1 ; − 1 , C 5 ; 0 ; − 2 . Tìm tọa độ điểm H sao cho tứ giác ABCH theo thứ tự đó lập thành hình thang cân với hai đáy AB, CH
A. H(3;-1;0)
B. H(7;1;-4)
C. H(-1;-3;4)
D. H(1;-2;2)
Trong không gian với hệ tọa độ Oxyz, cho các điểm A ( − 1 ; 0 ; l ) , B l ; 1 ; − l , C 5 ; 0 ; − 2 . Tìm tọa độ điểm H sao cho tứ giác ABCH theo thứ tự đó lập thành hình thang cân với hai đáy AB, CH .
A. H 3 ; − 1 ; 0
B. H 7 ; 1 ; − 4
C. H − 1 ; − 3 ; 4
D. H 1 ; − 2 ; 2
Đáp án C
Ta có:
A B → = 2 ; 1 ; − 2 A C → = 6 ; 0 ; − 3 ⇒ A B → ; A C → = 3 ; 6 ; 6 ⇒ d C ; A B = A B → ; A C → A B → = 3
Gọi M là hình chiếu của B trên H C ⇒ B M = 3.
Tam giác BMC vuông tại M, có M C = B C 2 − B M 2 = 3
Suy ra
H C = A B + 2. M C = 3 + 2.3 = 9 = 3 A B ⇒ C H → = 3 B A →
Mà B A → = − 2 ; − 1 ; 2 C H → = x − 5 ; y ; z + 2
suy ra x = 5 = 3. − 2 y = 3. − 1 z + 2 = 3.2 ⇔ x = − 1 y = − 3 z = 4
Vậy H − 1 ; − 3 ; 4 .
Trong không gian với hệ tọa độ Oxyz, cho các điểm A(-1;0;1), B(1;1;-1), C(5;0;-2). Tìm tọa độ điểm H sao cho tứ giác ABCH theo thứ tự đó lập thành hình thang cân với hai đáy AB, CH.
A. H(3;-1;0)
B. H(7;1;-4)
C. H(-1;-3;4)
D. H(1;-2;2)
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A − 2 ; 3 ; 1 , B 2 ; 1 ; 0 và C − 3 ; − 1 ; 1 . Tìm tất cả các điểm D sao cho ABCD là hình thang có đáy AD và S A B C D = 3 S Δ A B C .
A. D 8 ; 7 ; − 1
B. D − 8 ; − 7 ; 1 D 12 ; 1 ; − 3
C. D 8 ; 7 ; − 1 D − 12 ; − 1 ; 3
D. D − 12 ; − 1 ; 3
Đáp án D
Vì ABCD là hình thang ⇒ A D / / B C ⇒ u → A D = u → B C = − 5 ; − 2 ; 1
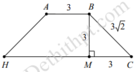
=>Phương trình đường thẳng AD là x + 2 − 5 = y − 3 − 2 = z − 1 1 ⇒ D − 5 t − 2 ; − 2 t + 3 ; t + 1
Ta có S A B C D = 3 S Δ A B C ⇔ S Δ A B C + S Δ A C D = 3 S Δ A B C ⇔ S Δ A C D = 2 S Δ A B C
Mà diện tích tam giác ABC là S Δ A B C = 1 2 A B ¯ ; A C ¯ = 341 2 ⇒ S Δ A C D = 341
Mặt khác A D ¯ ; A C ¯ = 341 t 2 ⇒ 1 2 341 t 2 = 341 ⇔ t = 2 t = − 2 ⇒ D − 12 ; − 1 ; 3 D 8 ; 7 ; − 1
Vì ABCD là hình thang → D − 12 ; − 1 ; 3
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(-2;3;1), B(2;1;0) và C(-3;-1;1). Tìm tất cả các điểm D sao cho ABCD là hình thang có đáy AD và S A B C D = 3 S A B C
A. D(8;7;-1)
B. [ D ( 12 ; 1 ; - 3 ) D ( 8 ; 7 ; - 1 )
C. [ D ( - 12 ; - 1 ; 3 ) D ( 8 ; 7 ; - 1 )
D. D(-12;-1;3)
Đáp án D
Vì ABCD là hình thang
![]()
=>Phương trình đường thẳng AD là
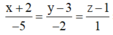
![]()
Ta có

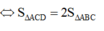
Mà diện tích tam giác ABC là
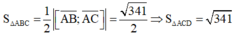
Mặt khác
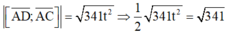

Vì ABCD là hình thang => D(-12;-1;3)
Trong không gian với hệ tọa độ Oxyz, cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật. Biết A(0;0;0), D(2;0;0), B(0; 4;0).
A. 2
B. 1 2
C. 2 2
D. 2