Chọn C.
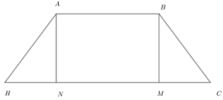
Phương pháp: Sử dụng các véc tơ bằng nhau.

Giả sử M,N lần lượt là hình chiếu của A, B lên CH.
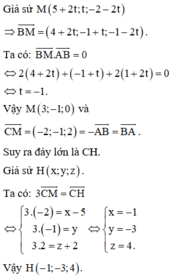
Chọn C.

Phương pháp: Sử dụng các véc tơ bằng nhau.

Giả sử M,N lần lượt là hình chiếu của A, B lên CH.
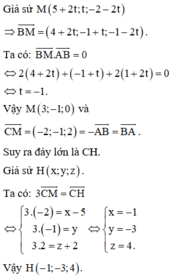
Trong không gian với hệ tọa độ Oxyz, cho các điểm A ( − 1 ; 0 ; l ) , B l ; 1 ; − l , C 5 ; 0 ; − 2 . Tìm tọa độ điểm H sao cho tứ giác ABCH theo thứ tự đó lập thành hình thang cân với hai đáy AB, CH .
A. H 3 ; − 1 ; 0
B. H 7 ; 1 ; − 4
C. H − 1 ; − 3 ; 4
D. H 1 ; − 2 ; 2
Trong không gian với hệ tọa độ Oxyz, cho các điểm A − 1 ; 0 ; 1 , B 1 ; 1 ; − 1 , C 5 ; 0 ; − 2 . Tìm tọa độ điểm H sao cho tứ giác ABCH theo thứ tự đó lập thành hình thang cân với hai đáy AB, CH
A. H(3;-1;0)
B. H(7;1;-4)
C. H(-1;-3;4)
D. H(1;-2;2)
Trong không gian với hệ tọa độ Oxyz, cho 3 điểm A(a;0;0), B(1;b;0), C(1;0;c), với a,b,c là các số thực thay đổi sao cho H(3;2;1) là trực tâm của tam giác ABC. Tính S=a+b+c.
A. S = 2
B. S = 19
C. S = 11
D. S = 9
Trong không gian với hệ tọa độ Oxyz, cho hình thang cân ABCD có AB là đáy lớn, CD là đáy nhỏ và A ( 3;-1;-2 ); B ( 1;5;1 ); C ( 2;3;3 ). Tìm tọa độ điểm D của hình thang cân.
A. D ( 4;3;0 )
B. D 164 49 ; 51 49 ; 48 49
C. D 1 2 ; 1 3 ; 1 4
D. D ( -4;3;0 )
Trong không gian với hệ trục tọa độ Oxyz, gọi H là hình chiếu vuông góc của điểm A(-3;-1;-1) lên mặt phẳng (P): 2x + y + z - 4 = 0. Tìm tọa độ điểm H
A. H(2;0;0)
B. H(1;2;0)
C. H(1;1;1)
D. H ( 1 2 ; 1 ; 2 )
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(0; 0; 2), B(3; 0; 5), C(1; 1; 0). Tọa độ của điểm D sao cho ABCD là hình bình hành là
A. D(4; 1; 3)
B. D(-4; -1; -3)
C. D(2; 1; -3)
D. D(-2; 1; -3)
Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD có tọa độ các điểm A(1;1;1), B(2;0;2), C(-1;-1;0), D(0;3;4). Trên các cạnh AB, AC, ADlần lượt lấy các điểm B’,C’,D’ sao cho A B A B ' + A C A C ' + A D A D ' = 4 và tứ diện AB’C’D’ có thể tích nhỏ nhất. Phương trình mặt phẳng (B’C’D’) là
A. 16x-40y-44z-39=0.
B. 16x-40y-44z+39=0.
C. 16x+40y+44z-39=0.
D. 16x+40y-44z+39=0.
Trong không gian với hệ tọa độ Oxyz, cho điểm H(1;2;-3). Tìm phương trình mặt phẳng α cắt các trục tọa độ Ox, Oy, Oz lần lượt tại 3 điểm A, B, C sao cho H là trực tâm tam giác ABC.
A. α : x+2y-3z-14=0
B. α : x+2y-3z+4=0
C. α : 6x+3y-2z-18=0
D. α : 6x+3y-2z+8=0
Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD có tọa độ các điểm A 1 ; 1 ; 1 , B 2 ; 0 ; 2 , C - 1 ; - 1 ; 0 , D 0 ; 3 ; 4 . Trên các cạnh AB, AC, AD lần lượt lấy các điểm B ' , C ' , D ' sao cho A B A B ' + A C A C ' + A D A D ' = 4 và tứ diện A B ' C ' D ' có thể tích nhỏ nhất. Phương trình măt phẳng B ' C ' D ' là
A. 16 x - 40 y - 44 z + 39 = 0
B. 16 x + 40 y + 44 z - 39 = 0
C. 16 x + 40 y - 44 z + 39 = 0
D. 16 x - 40 y - 44 z - 39 = 0