Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD có tọa độ các điểm A 1 ; 1 ; 1 , B 2 ; 0 ; 2 , C - 1 ; - 1 ; 0 , D 0 ; 3 ; 4 . Trên các cạnh AB, AC, AD lần lượt lấy các điểm B ' , C ' , D ' sao cho A B A B ' + A C A C ' + A D A D ' = 4 và tứ diện A B ' C ' D ' có thể tích nhỏ nhất. Phương trình măt phẳng B ' C ' D ' là
A. 16 x - 40 y - 44 z + 39 = 0
B. 16 x + 40 y + 44 z - 39 = 0
C. 16 x + 40 y - 44 z + 39 = 0
D. 16 x - 40 y - 44 z - 39 = 0
Chọn đáp án C
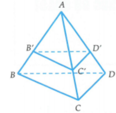
Áp dụng công thức tỉ số thể tích ta có:
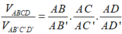
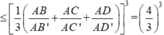
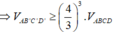
Suy ra thể tích tứ diện AB'C'D' nhỏ nhất khi
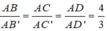
Khi đó A B ' ⇀ = 3 4 A B ⇀ và B ' C ' D ' / / B C D
⇒ Mặt phẳng B ' C ' D ' có một vec-tơ pháp tuyến là
![]()
Lại có
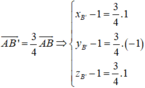
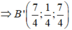
Phương trình mặt phẳng B ' C ' D '
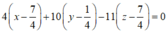
![]()



