Cho hai góc m O n ^ và t O n ^ phụ nhau, biết t O n ^ = 60 ° .
a) Tính số đo m O n ^ .
b) Trên nửa mặt phẳng bờ Om không chứa tia On vẽ tia Ox sao cho m O x ^ = 30 ° . Tia On có phải là tia phân giác của x O t ^ không? Tại sao
Cho điểm O nằm giữa A và B;điểm M nằm giữa hai điểm A và O;điểm N nằm giữa hai điểm B và O.
a,Nêu tên các tia trùng nhau góc O
b,CMR:điểm O nằm giữa M và N
Dòng điện thẳng dài I và hai điểm M, N nằm trong cùng mặt phẳng, nằm hai phía so với dòng điện sao cho MN vuông góc với dòng điện. Gọi O là điểm thuộc đoạn MN sao cho OM = 1,5ON. Nếu độ lớn cảm ứng từ tại M và N lần lượt là B M = 2 , 8 . 10 - 5 T , B N = 4 , 8 . 10 - 5 T thì độ lớn cảm ứng từ tại O là
A. 3 , 36 . 10 - 5 T
B. 16 , 8 . 10 - 5 T
C. 3 , 5 . 10 - 5 T
D. 56 . 10 - 5 T
Cho hình trụ (T) có hai hình tròn đáy là (O) và (O'). Xét hình nón (N) có đỉnh O', đáy là hình tròn (O) và đường sinh hợp với đáy một góc α . Biết tỉ số giữa diện tích xung quanh hình trụ (T) và diện tích xung quanh hình nón (N) bằng 3 . Tính số đo góc α .
![]()
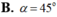
![]()
![]()
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Một đường thẳng d đi qua B cắt (O) tại điểm thứ hai M và cắt (O') tại điểm thứ hai N. Các tiếp tuyến của (O) tại M và của (O') tại N cắt nhau tại điểm P.
a. Cho biết ∠MAN = α. Tính ∠MPN theo α
b. Chứng minh rằng ∠OAO' = 90o khi và chỉ khi ΔMNP vuông tại P
Cho đường tròn tâm O(0;0) đường kính AB = 4. Trên AB lấy hai điểm M,N đối xứng với nhau qua O sao cho MN = 2. Qua M, N kẻ hai dây cung CD và EF cùng vuông góc với AB. Tính diện tích hình phẳng giới hạn bởi đường tròn và hai dây cung CD, EF (phần không chứa điểm O).
A. S = 4 π 3 − 3
B. S = 4 π − 2 3
C. S = 8 π 3 − 2 3
D. S = 4 π 3 + 2 3
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Tiếp tuyến tại A của đường tròn (O) cắt (O') tại C, của đường tròn (O') cắt (O) tại D. AB cắt CD tại M, N là trung điểm CD. Chứng minh góc CAM bằng góc DAN.
Cho đường tròn(O;R) có hai đường kính AB và CD vuông góc với nhau.Trên đoạn thẳng AB lấy một điểm M(khác O).Đường thẳng CM cắt đường tròn (O) tại điểm thứ hai N.Đường thẳng vuông góc với AB tại M cắt tiếp tuyến tại N của đường tròn (O) ở điểm P.Chứng minh rằng:
a)Tứ giác OMNP nội tiếp được
b)Tứ giác CMPO là hình bình hành
c)Tích CM.CN không phụ thuộc vào vị trí của điểm M trên đoạn thẳng AB
a: góc OMP=góc ONP=90 độ
=>OMNP nội tiếp
b: MP//OC(cùng vuông góc AB)
=>góc MCO=góc NMP
góc NMP=góc MNO
=>góc MNO=góc MCO
=>góc MNO=góc ODN
=>CM//OP
Xét tứ giác CMPO có
CM//PO
CO//PM
=>CMPO là hình bình hành
c: Xét ΔCOM vuông tại O và ΔCND vuông tại N có
góc OCM chung
=>ΔCOM đồng dạng với ΔCND
=>CO/CN=CM/CD
=>CN*CM=CO*CD=2R^2 ko phụ thuộc vào vị trí của M
Bài 1: Cho (O;R) và một điểm M. Hãy chỉ dùng thước thẳng dựng đường thẳng đi qua M và vuông góc với đường kính AB cho trước (đường kính AB không đi qua M).
Bài 2: Cho (O;R) và (O’;R’) cùng trực giao với đường tròn (C;r). Chứng minh trục đẳng phương của hai đường tròn (O;R) và (O’;R’) đi qua điểm C.
Bài 3: Cho A không thuộc (O;R). O’ di động trên (O;R), đường thằng a là trục đẳng phương của hai đường tròn (O;R) và (O’;O’A). Chứng minh khoảng cách từ A đến đường thẳng a là không đổi.
Bài 4: Cho góc xOy = 45 độ. A là một điểm thuộc miền trong của góc đó. Bằng thước và compa hãy dựng đường thẳng đi qua A cắt Ox, Oy lần lượt tại M, N sao cho A là trung điểm của MN.
Bài 5: Cho góc xAy, hai điểm B, C lần lượt thay đổi trên các tia Ax, Ay sao cho AB+AC=d không đổi. Từ A kẻ đường thẳng song song với BC, cắt đường tròn ngoại tiếp tam giác ABC tại M. Tìm quỹ tích điểm M.
Bài 6: Cho nửa (T) đường kính AB, hai nửa đường thẳng Ax, By nằm cùng một phía và tiếp xúc với (T). Lấy hai điểm di động M thuộc Ax, N thuộc By sao cho ABMN có diện tích S không đổi. Tìm quỹ tích hình chiếu trung điểm I của AB trên MN.
Bài 7: Cho ∆ABC, các điểm M, N lần lượt thuộc AB, AC sao cho MN // BC. Xác định trục đẳng phương của 2 đường tròn đường kính BN và CM.
chia nhỏ ra thôi . Nhiều này nhìn hoa mắt làm sao nổi.
Cho góc xOy. Trên tia Ox, Oy tương ứng lấy hai điểm A và B khác O sao cho OA=OB. Vẽ hai đường tròn tâm A và B có cùng bán kính sao cho chúng cắt nhau M và N nằm trong góc xOy. Chứng minh:
a) Ba điểm O, M, N thẳng hàng
b) Mn là tia phân giác của góc AMB
Trên đường thẳng xy , lấy điểm O . Trên cùng nửa mặt phẳng bờ là đường thẳng xy vẽ 2 tia Om và On sao cho hai góc \(x\widehat{O}m\) và \(y\widehat{O}n\) là hai góc phụ nhau và \(x\widehat{O}m\) = \(56^0\)
a ) Tính góc \(y\widehat{O}n\)
b ) Tính góc kề bù với góc \(x\widehat{O}m\)
c ) Tính góc kề bù với góc \(y\widehat{O}n\)
Giúp mk với nha các bạn