Cho hàm số f(x)=| 2 x 3 - 3 x 2 + m |. Có bao nhiêu số nguyên m để m i n [ - 1 ; 3 ] f ( x ) ≤ 3
A. 4.
B. 8.
C. 31.
D. 39
1/ Cho hàm số \(f\)(\(x\))=\(\dfrac{1}{3}\)\(x\)\(^3\)+\(x \)\(^2\)-(\(m\)+1)\(x\)-\(m\)+3. Với \(m\) là tham số. Có bao nhiêu số nguyên \(m\) thuộc đoạn [-10;10] để \(f\)'(\(x\)) ≥ 0, ∀\(x\) ϵ \(R\)
2/ Cho hàm số \(y\) = \(\dfrac{mx+4}{x+m}\). Với \(m\) là tham số. Có bao nhiêu số nguyên m thuộc đoạn [-5;2023] để \(y\)' > 0, ∀\(x\) ϵ (0;+∞).
1: \(f'\left(x\right)=\dfrac{1}{3}\cdot3x^2+2x-\left(m+1\right)=x^2+2x-m-1\)
\(\Delta=2^2-4\left(-m-1\right)=4m+8\)
Để f'(x)>=0 với mọi x thì 4m+8<=0 và 1>0
=>m<=-2
=>\(m\in\left\{-10;-9;...;-2\right\}\)
=>Có 9 số
Cho hàm số y=f(x) có đạo hàm f'(x)= x ( x - 1 ) 2 ( x 2 + m x + 9 ) . Có bao nhiêu số nguyên dương m để hàm số y=f(3-x) đồng biến trên khoảng ( 3 ; + ∞ ) .
A. 6.
B. 8.
C. 5.
D. 7.
Cho hàm số y = f(x) xác định trên tập số thực R và có đạo hàm f'(x) = (x - sinx)(x- m- 3)(x- \(\sqrt{9-m^2}\) )3 ∀x∈ R (m là tham số). Có bao nhiêu giá trị nguyên của m để hàm số y =f(x) đạt cực tiểu tại x = 0
\(f'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x-sinx=0\\x-m-3=0\\x-\sqrt{9-m^2}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=m+3\\x=\sqrt{9-m^2}\end{matrix}\right.\)
Do hệ số bậc cao nhất của x dương nên:
- Nếu \(m=-3\Rightarrow f'\left(x\right)=0\) có nghiệm bội 3 \(x=0\) \(\Rightarrow x=0\) là cực tiểu (thỏa mãn)
- Nếu \(m=3\Rightarrow x=0\) là nghiệm bội chẵn (không phải cực trị, ktm)
- Nếu \(m=0\Rightarrow x=3\) là nghiệm bội chẵn và \(x=0\) là nghiệm bội lẻ, đồng thời \(x=0\) là cực tiểu (thỏa mãn)
- Nếu \(m\ne0;\pm3\) , từ ĐKXĐ của m \(\Rightarrow-3< m< 3\Rightarrow\left\{{}\begin{matrix}m+3>0\\\sqrt{9-m^2}>0\end{matrix}\right.\)
Khi đó \(f'\left(x\right)=0\) có 3 nghiệm pb trong đó \(x=0\) là nghiệm nhỏ nhất
Từ BBT ta thấy \(x=0\) là cực tiểu
Vậy \(-3\le m< 3\)
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = x ( x - 2 ) 2 ( 2 x + m + 1 ) ∀ x ∈ ℝ Có bao nhiêu số nguyên âm m để hàm số g ( x ) = f ( x 2 ) đồng biến trên khoảng
A. 5
B. 2
C. 3
D. 4
Cho hàm số f ( x ) = ∫ 1 x t 3 - ( m + 2 ) t 2 + 2 ( m + 1 ) t - 4 t 4 + 1 d t với x > 1. Trong [-10;10] có bao nhiêu giá trị nguyên của tham số thực m để hàm số đã cho có 3 điểm cực trị
A. 14
B. 15
C. 16
D. 17
Cho hàm số f ( x ) = | x 3 - 3 x 2 + m | . Có bao nhiêu số nguyên m để m i n [ 1 ; 3 ] f ( x ) ≤ 3 .
A. 4.
B. 10.
C. 6.
D. 11.
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = x ( x - 2 ) 2 ( 2 x + m + 1 ) với mọi x ∈ R . Có bao nhiêu số nguyên âm m để hàm số g ( x ) = f ( x 2 ) đồng biến trên khoảng ?
A. 5.
B. 2.
C. 3.
D. 4.
Cho hàm số f(x) = (m - 1)x3 - 5x2 + (m+3)x + 3. Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y = f(\(\left|x\right|\)) có đúng 3 điểm cực trị?
- Với \(m=1\) thỏa mãn
- Với \(m\ne1\):
\(f'\left(x\right)=3\left(m-1\right)x^2-10x+m+3\)
\(f\left(\left|x\right|\right)\) có số cực trị bằng \(2k+1\) với \(k\) là số cực trị dương của \(f\left(x\right)\) nên hàm có 3 cực trị khi \(f'\left(x\right)=0\) có đúng 1 nghiệm dương
TH1: \(f'\left(x\right)=0\) có 1 nghiệm bằng 0 \(\Rightarrow m=-3\Rightarrow f'\left(x\right)=-12x^2-10x\) ko có nghiệm dương (loại)
TH2: \(f'\left(x\right)=0\) ko có nghiệm bằng 0 nào \(\Rightarrow f'\left(x\right)=0\) khi và chỉ khi nó có 2 nghiệm trái dấu
\(\Rightarrow ac< 0\Leftrightarrow3\left(m-1\right)\left(m+3\right)< 0\)
\(\Rightarrow-3< m< 1\)
Vậy \(-3< m\le1\)
Cho hàm số y=f(x) liên tục trên ℝ ,f(2)=3 và có đồ thị như hình vẽ bên
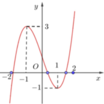
Có bao nhiêu số nguyên m ∈ - 20 ; 20 để phương trình có 4 nghiệm thực phân biệt. f ( x + m ) = 3
A. 2
B. 18
C. 4
D. 19