Đồ thị của hàm số y = x + 3 x 2 + 1 có tất cả bao nhiêu tiệm cận ngang
A. 0
B. 1
C. 2
D. 3
Cho hàm số y= 2+ x, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = 2 - x, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = x - 2, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = x + 2, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y= 2+ x, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = 2 - x, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = x - 2, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = x + 2, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Bài 1 a) Khảo sát và vẽ đồ thị hàm số y=x³-2x²+x (C) b) từ đồ thị (C) suy ra đồ thị các hàm số sau: y=|x³-2x²+x|, y=|x|³ -2x²+|x| Bài 2: Khảo sát và vẽ đồ thị hàm số y=x⁴-2x²-3 (C). Từ đồ thị (C) suy ra đồ thị hàm số y=|y=x⁴-2x²-3|
Cho hàm số y = (m-2)x + m + 3
1. Tìm điều kiện của m để hàm số luôn nghịch biến
2. Tìm m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 3
3. Tìm m để đồ thị hàm số trên và các đồ thị hàm số y= -x+2; y = 2x-1 đồng quy
1. hàm số nghịch biến khi
\(a< 0\\ \Leftrightarrow m-2< 0\\ \Leftrightarrow m< 2\)
2. \(y=\left(m-2\right)x+m+3\cap Ox,tại,x=3\)
\(\Rightarrow y=0\)
Có: \(0=\left(m-2\right)3+m+3\\ \Leftrightarrow0=4m-4\\ \Leftrightarrow m=\dfrac{3}{4}\)
3. pt hoành độ giao điểm của
\(y=-x+2,và,y=2x-1\) là
\(-x+2=2x-1\\ \Leftrightarrow3x=3\Leftrightarrow x=1\Rightarrow y=1\)
A(1,1)
3 đt đồng quy \(\Rightarrow A\in y=\left(m-2\right)x+m+3\\ \Rightarrow1=\left(m-2\right)1+m+3\\ \Leftrightarrow2m=0\\ \Leftrightarrow m=0\)
Cho hàm số y = - 3x + 2 (d) a) Vẽ đồ thị (d) của hàm số trên. b) Tìm m để đồ thị hàm số y = (m+1)x - 3 song song với đồ thị hàm số y = - 3x + 2.
a: 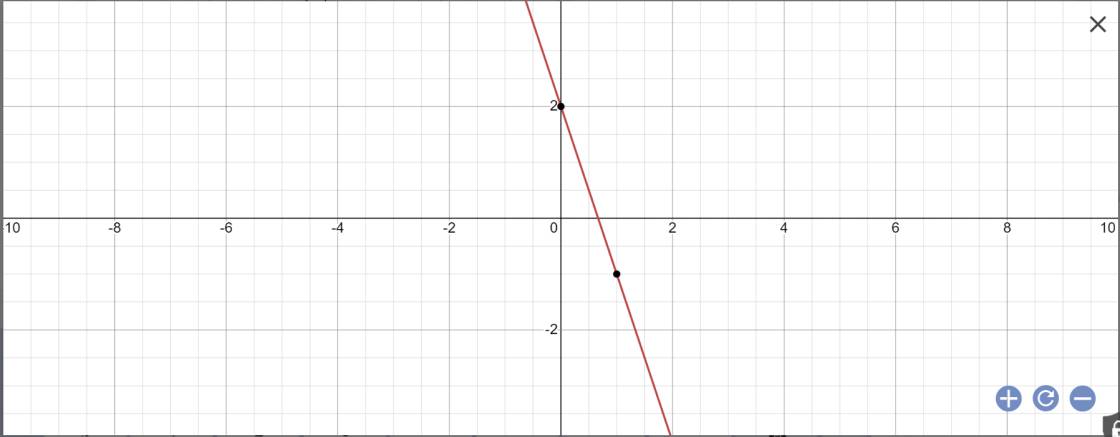
b: Để đồ thị hàm số y=(m+1)x-3 song song với đồ thị hàm số y=-3x+2 thì \(\left\{{}\begin{matrix}m+1=-3\\2\ne-3\left(đúng\right)\end{matrix}\right.\)
=>m+1=-3
=>m=-4
cho hàm số y = f ( x ) = ax
a , Xác định đồ thị hàm số biết đồ thị của hàm số đi qua điểm ( 3 , - 42)
b Cho hàm số y = g(x) = 100- 3 . x3
Tính g(-2 ) ; g( 3 )
a: Thay x=3 và y=-42 vào y=ax, ta được:
3a=-42
hay a=-14
a) khảo sát và vẽ đồ thị hàm số \(y=\dfrac{2x-3}{x+2}\)
b) khảo sát và vẽ đồ thị hàm số \(y=\left|\dfrac{2x-3}{x+2}\right|\)
c) khảo sát và vẽ đồ thị hàm số \(y=\dfrac{2x-3}{\left|x+2\right|}\)
Cho hàm số y=f(x)=x^3+ax^2+bx+4 có đồ thị (C) như hình vẽ. Hỏi (C) là đồ thị của hàm số y=f(x) nào?
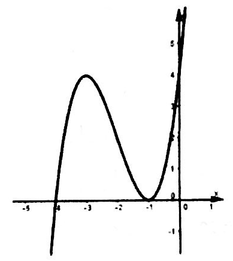
A. y = f ( x ) = x 3 - 3 x 2 + 4
B. y = f ( x ) = x 3 + 6 x 2 + 9 x + 4
C. y = f ( x ) = x 3 + 3 x 2 + 4
D. y = f ( x ) = x 3 - 6 x 2 + 9 x + 4
tìm m thỏa mãn yêu cầu bài toán
a) đồ thị hàm số \(y=\dfrac{x+3}{2x+3m}\) có đường tiệm cận đứng đi qua điểm M (3;-1)
b) đường thẳng x = -2 là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{2x-3}{x+m}\)
c) biết đồ thị hàm số \(y=\dfrac{ax+1}{bx-2}\) có tiệm cận đứng là x = 2 và tiệm cận ngang y = 3. Tính 2a+3b
d) đồ thị hàm số \(y=\dfrac{x+2}{x^2+2x+m^2-3m}\) có 2 đường tiệm cận đứng
a: \(\lim\limits_{x\rightarrow-\dfrac{3m}{2}}\dfrac{x+3}{2x+3m}=\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow-\dfrac{3m}{2}}2x+3m=0\\\lim\limits_{x\rightarrow-\dfrac{3m}{2}}x+3=\dfrac{-3m}{2}+3\end{matrix}\right.\)
=>x=-3m/2 là tiệm cận đứng duy nhất của đồ thị hàm số \(y=\dfrac{x+3}{2x+3m}\)
Để tiệm cận đứng của đồ thị hàm số \(y=\dfrac{x+3}{2x+3m}\) đi qua M(3;-1) thì \(-\dfrac{3m}{2}=3\)
=>-1,5m=3
=>m=-2
b: \(\lim\limits_{x\rightarrow-m}\dfrac{2x-3}{x+m}=\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow-m}2x-3=-2m-3\\\lim\limits_{x\rightarrow-m}x+m=0\end{matrix}\right.\)
=>x=-m là tiệm cận đứng duy nhất của đồ thị hàm số \(y=\dfrac{2x-3}{x+m}\)
Để x=-2 là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{2x-3}{x+m}\) thì -m=-2
=>m=2
c: \(\lim\limits_{x\rightarrow\dfrac{2}{b}}\dfrac{ax+1}{bx-2}=\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow\dfrac{2}{b}}ax+1=a\cdot\dfrac{2}{b}+1\\\lim\limits_{x\rightarrow\dfrac{2}{b}}bx-2=b\cdot\dfrac{2}{b}-2=0\end{matrix}\right.\)
=>Đường thẳng \(x=\dfrac{2}{b}\) là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{ax+1}{bx-2}\)
=>2/b=2
=>b=1
=>\(y=\dfrac{ax+1}{x-2}\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{ax+1}{x-2}=\lim\limits_{x\rightarrow+\infty}\dfrac{a+\dfrac{1}{x}}{1-\dfrac{2}{x}}=a\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{ax+1}{x-2}=\lim\limits_{x\rightarrow-\infty}\dfrac{a+\dfrac{1}{x}}{1-\dfrac{2}{x}}=a\)
=>Đường thẳng y=a là tiệm cận ngang của đồ thị hàm số \(y=\dfrac{ax+1}{x-2}\)
=>a=3
Bài 1 :Cho hàm số y=(m-1)x+m+3
1, Tìm giá trị của m để đồ thị hàm số song song với đồ thị hàm số y=-2x+1
2, Tìm giá trị của m để đồ thị hàm số đi qua điểm (1;-4)
3, Tìm điểm cố định mà đồ thị của hàm số luôn đi qua\
Bài 2 : Cho hàm số y=(2m-1)x+m-3
1, Tìm m để đồ thị hàm số đi qua điểm (2;5)
2, Cmr đồ thị hàm số luôn đi qua 1 điểm cố định với mọi m. Tìm điểm cố định ấy
3, Tìm m để đồ thị hàm số cắt trục hoành tai điểm có hoành độ \(x=\sqrt{2}-1\)