a: Có 1 đường duy nhất

b: Đường thẳng d cắt (P) tại 1 giao điểm

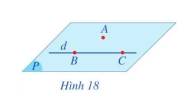
a) Mặt phẳng đi qua ba điểm A, B, C đi qua đường thẳng d

b) Có một và chỉ một mặt phẳng đi qua điểm A và đường thẳng d

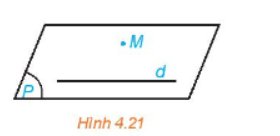
a) Có duy nhất một đường thẳng đi qua M song song với d

b) Nếu một đường thẳng đi qua M và song song với d thì đường thẳng đó có thuộc mặt phẳng (P) vì hai đường thẳng song song đồng phẳng

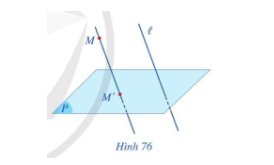
Qua mỗi điểm M trong không gian, có duy nhất một đường thẳng song song hoặc trùng với đường thẳng ℓ. Đường thẳng đó và mặt phẳng (P) có 1 điểm chung.

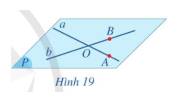
a) Mặt phẳng đi qua ba điểm A. B, O đi qua hai đường thẳng a và b

b) Có một và chỉ một mặt phẳng đi qua hai đường thẳng a và b

Chọn đáp án D

Giả sử mặt phẳng (P) có vectơ pháp tuyến là n ⇀ = a ; b ; c a 2 + b 2 + c 2 ≠ 0 .

Khi đó phương trình mặt phẳng (P) có dạng a x + b y + c z + d = 0 .

Do M 0 ; 0 ; 1 ∈ P  nên c + d = 0 ⇔ d = - c  

Do  N 0 ; 3 ; 1 ∈ P  nên   3 b + c + d = 0 ⇔ b = 0

Khi đó P : a x + c z - c = 0  

Từ giả thiết ta có d B ; P = 2 d A ; P

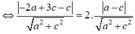
⇔ - 2 a + 2 c a 2 + c 2 = 2 a - c a 2 + c 2  (luôn đúng). Vậy có vô số mặt phẳng (P) thỏa mãn.