Có bao nhiêu giá trị nguyên của tham số m để phương trình m x 2 + 2 x 3 − 2 x 2 − 4 x + 2 = 0 có nghiệm đúng với mọi x ≤ − 3 ?
A. 4
B. Không có giá trị nào của m
C. Vô số giá trị của m
D. 6
Có bao nhiêu giá trị nguyên của tham số m để phương trình x^2 -2|x| +1-m = 0 có 4 nghiệm phân biệt ?
Đặt \(\left|x\right|=t\ge0\)
\(\Rightarrow t^2-2t+1-m=0\) (1)
Phương trình (1) là bậc 2 nên có đối đa 2 nghiệm t
Với mỗi giá trị \(t>0\) cho 2 nghiệm x tương ứng nên pt đã cho có 4 nghiệm pb khi và chỉ khi (1) có 2 nghiệm dương phân biệt
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=1-\left(1-m\right)>0\\t_1+t_2=2>0\\t_1t_2=1-m>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\m< 1\end{matrix}\right.\) \(\Leftrightarrow0< m< 1\)
Cho phương trình 4 6 + x - x 2 - 3 x = m x + 2 + 2 3 - x với m là tham số. Hỏi có bao nhiêu giá trị nguyên của m để phương trình có nghiệm?
A. 10
B. 9
C. 11
D. 8
Chọn đáp án A
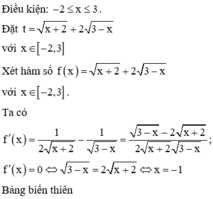
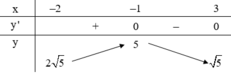

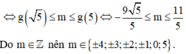
Vậy số giá trị nguyên của m để phương trình có nghiệm là 10.
Có bao nhiêu giá trị nguyên của tham số m để phương trình x^2 -2|x| +1-m = 0 có 4 nghiệm phân biệt ?
Cho phương trình: sinx(2-cos2x) - 2(2 cos 3 x + m + 1 ) 2 cos 3 x + m + 2 = 3 2 cos 3 x + m + 2 . Có bao nhiêu giá trị nguyên của tham số m để phương trình trên có đúng 1 nghiệm x ∈ 0 ; 2 π 3 ?
A. 1
B. 4
C. 2
D. 3
Đáp án là B
Phương trình tương đương với
![]()
![]()
![]()
Xét hàm ![]() Ta có
Ta có ![]() đồng biến
đồng biến
Mà ![]() suy ra
suy ra
![]()
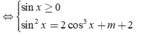
![]()
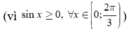
![]()
![]()
Đặt u = cosx, 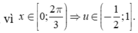
Khi đó phương trình trở thành ![]()
Xét ![]()
![]()
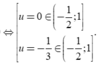
Bảng biến thiên
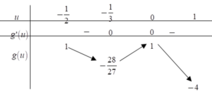
Dựa vào bảng biến thiên suy ra phương trình có nghiệm khi
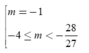
![]()
Có bao nhiêu giá trị nguyên của tham số m để phương trình 1 + 2 cos x + 1 + 2 sin x = 1 2 m có nghiệm?
A. 3.
B. 5.
C. 4.
D. 2.
Cho phương trình:
sin 3 x + 2 sin x + 3 = 2 c o s 3 x + m 2 c o s 3 x + m - 2 + 2 c o s 3 x + c o s 2 x + m .
Có bao nhiêu giá trị nguyên của tham số m để phương trình trên có đúng 1 nghiệm x ∈ 0 ; 2 π 3 ?
A. 2
B. 1
C. 3
D. 4
Có bao nhiêu giá trị nguyên của tham số m để phương trình 6 + x - 2 - x - 3 + x - 6 - x - 5 - m = 0 có nghiệm thực
A. 0
B. 2
C. 3
D. 1
Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng (-1;7) để phương trình ( m - 1 ) x + ( m + 2 ) x ( x 2 + 1 ) = x 2 + 1 có nghiệm?
A. 6
B. 7
C. 1
D. 5
Có bao nhiêu giá trị nguyên của tham số m để phương trình
\(\sqrt{x+2}+\sqrt{2-x}+2\sqrt{4-x^2}+2m+3=0\) có nghiệm
ĐK: \(-2\le x\le2\)
Đặt \(\sqrt{x+2}+\sqrt{2-x}=t\left(2\le t\le2\sqrt{2}\right)\)
Phương trình đã cho trở thành:
\(t+t^2-4+2m+3=0\)
\(\Leftrightarrow2m=f\left(t\right)=-t^2-t+1\)
Phương trình đã cho có nghiệm khi \(minf\left(t\right)\le2m\le maxf\left(t\right)\)
\(\Leftrightarrow-7-2\sqrt{2}\le2m\le-5\)
\(\Leftrightarrow\dfrac{-7-2\sqrt{2}}{2}\le m\le-\dfrac{5}{2}\)
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-20;20] để phương trình \(\sqrt{2x^2-8x+m}=x-1\) có nghiệm duy nhất
\(\sqrt{2x^2-8x+m}=x-1\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x^2-8x+m=\left(x-1\right)^2\\x-1\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2-6x+m-1=0\\x\ge1\end{matrix}\right.\)
Yêu cầu bài toán thỏa mãn khi phương trình \(x^2-6x+m-1=0\left(1\right)\) có nghiệm duy nhất thỏa mãn \(x\ge1\)
\(\left(1\right)\Leftrightarrow m=f\left(x\right)=-x^2+6x+1\)
Đồ thi hàm số \(y=f\left(x\right)=-x^2+6x+1\):
Dựa vào đồ thị ta được \(m=10\)
P/s: Cái này t lười vẽ bảng biến thiên nên vẽ đồ thị đó, chứ bình thường viết trong vở thì dùng bảng biến thiên nhanh hơn nhiều.