Gọi C n k và A n k lần lượt là tổ hợp chập k của n và chỉnh hợp chập k của n. Tìm khẳng định sai trong các khẳng định sau:
![]()
![]()
![]()
![]()
Biết A n k , C n k , P n lần lượt là số chỉnh hợp chập k, số tổ hợp chập k và số hoán vị của n phần tử. Khẳng định nào sau đây sai?
A. P n = n !
B. C n k = C n n - k
C. C n k - 1 + C n k = C n + 1 k
D. A n k = C n k k !
Biết A n k , C n k , P n lần lượt là số chỉnh hợp chập k, số tổ hợp chập k và số hoán vị của n phần tử. Khẳng định nào sau đây sai?
A. P n = n !
B. C n k
C. C n k - 1 + C n k = C n + 1 k
D. A n k = C n k k !
Phân biệt sự khác nhau giữa một chỉnh hợp chập k của n phần tử và một tổ hợp chập k của n phần tử.
Chỉnh hợp chập k của n phần tử là một tập hợp con k phần tử của một tập hợp n phần tử được sắp xếp theo một thứ tự nào đó.
Tổ hợp chập k của n phần tử là tập hợp con k phần tử của một tập hợp n phần tử không để ý đến thứ tự các phần tử của tập hợp con đó.
Phân biệt sự khác nhau giữa một chỉnh hợp chập k của n phân tử và một tổ hợp chập k của n phân tử ?
|
Cho tập hợp A có n phần tử (n ≥ 1) |
||
|
Chỉnh hợp chập k của n phần tử |
Sắp xếp thứ tự các phần tử |
_ Sử dụng k phần tử trong số n phần tử của A (k ≤ n) và sắp xếp thứ tự k phần tử này (mỗi cách sắp xếp là một chỉnh hợp chập k của phần tử) _ Số chỉnh hợp chập k của n phần tử là:\(A^k_n=\dfrac{n!}{\left(n-k\right)!}\)
|
|
Tổ hợp chập k của n phần tử |
Không chú ý đến thứ tự của các phần tử |
_ Sử dụng k phần tử trong n phần tử A (k ≤ n) và không để ý đến thứ tự của các phần tử này. _Số tổ hợp chập k của n phần tử là: \(C^k_n=\dfrac{n!}{k!\left(n-k\right)!}\)
|
Viết công thức tính số chỉnh hợp chập k của n phần tử, công thức tính số tổ hợp chập k của n phần tử. Cho ví dụ.
+ Số chỉnh hợp chập k của n phần tử:
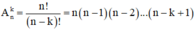
+ Số tổ hợp chập k của n phần tử:
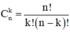
+ Ví dụ:
- Số chỉnh hợp chập 3 của 5: 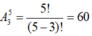
- Số tổ hợp chập 3 của 5: 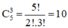
- Chọn ngẫu nhiên 5 bông hoa trong số 8 bông hoa khác nhau để cắm vào 5 lọ khác nhau:
⇒ Có 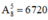 cách chọn.
cách chọn.
- Chọn ngẫu nhiên 5 bông hoa trong số 8 bông hoa khác nhau
⇒ Có 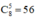 cách chọn.
cách chọn.
Tìm số nguyên dương n thỏa mãn các điều kiện sau C n - 1 4 - C n - 1 3 < 5 4 A n - 2 2 C n + 1 n - 4 ≥ 7 15 A n + 1 3
(Ở đây A n k , C n k lần lượt là số chỉnh hợp và số tổ hợp chập k của n phần tử).
A. n=7
B. n=8
C. n=9
D. n=10
Tìm số nguyên dương n thỏa mãn các điều kiện sau
C n - 1 4 - C n - 1 3 < 5 4 A n - 2 2 C n + 1 n - 4 ≥ 7 15 A n + 1 3
(Ở đây A n k ; C n k lần lượt là số chỉnh hợp và số tổ hợp chập k của n phần tử).
A. n = 7
B. n = 8
C. n = 9
D. n = 10
Điều kiện: n - 1 ≥ 4 nên n ≥ 5
Hệ điều kiện ban đầu tương đương:
⇔ n - 1 n - 2 n - 3 n - 4 4 . 3 . 2 . 1 - n - 1 n - 2 n - 3 3 . 2 . 1 ≤ 5 4 n - 2 n - 3 n + 1 n n - 1 n - 2 n - 3 5 . 4 . 3 . 2 . 1 ≥ 7 15 n + 1 n n - 1 ⇔ n 2 - 9 n - 22 < 0 n ≥ 5 n 2 - 5 n - 50 ≥ 0 ⇒ n = 10
Vậy n = 10 thỏa yêu cầu bài toán
Đáp án D
Với k và n là hai số nguyên dương tùy ý thỏa mãn k ≤ n. Công thức tính số tổ hợp chập k của n phần tử là
A . C n k = n ! ( n - k ) ! k !
B . A n k = n ! ( n - k ) !
C . C n k = n ! ( n - k ) !
D . A n k = n ! ( n - k ) ! k !
Chọn A
Công thức tính số tổ hợp chập k của n phần tử là: 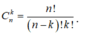
Cho tập A có n phần tửv( n > 2 ) k là một số nguyên 0<k<n Số chỉnh hợp chập k của n phần tử là