Đạo hàm của hàm số y = x 4 - 3 x 2 - 11 là
A. Hàm vừa chẵn, vừa lẻ
B. Hàm chẵn
C. Hàm không chẵn, không lẻ
D. Hàm lẻ
Những câu hỏi liên quan
Hàm số y=sin(x-\(\dfrac{\pi}{2}\))là
a hàm số chẵn
b hàm số lẻ
chàm số không chẵn không lẻ
d hàm số vừa chẵn vừa lẻ
.có thể giải chi tiết hệ mk đc ko.
\(y=sin\left(x-\dfrac{\pi}{2}\right)=-sin\left(\dfrac{\pi}{2}-x\right)=-cosx\)
\(y\left(-x\right)=-cos\left(-x\right)=-cosx=y\left(x\right)\)
Hàm đã cho là hàm chẵn
Đúng 4
Bình luận (1)
Hàm số f(x) = x (x4 - 3x2 -5) là :
A.Hàm số vừa chẵn, vừa lẻ B.Hàm số chẵn
C.Hàm số không chẵn, không lẻ D.Hàm số lẻ
Quan sát đồ thị hàm số y sin x ở Hình 25.a) Nêu tập giá trị của hàm số y sin xb) Gốc tọa độ có là tâm đối xứng của đồ thị hàm số không? Từ đó kết luận tính chẵn, lẻ của hàm số y sin xc) Bằng cách dịch chuyển đồ thị hàm số y sin x trên đoạn left[ { - pi ;pi } right] song song với trục hoành sang phải theo đoạn có độ dài 2pi , ta có nhận được đồ thị hàm số y sin x trên đoạn left[ {pi ;3pi } right] hay không? Hàm số y sin xcó tuần hoàn hay không/d) Tìm khoảng đồng biến, nghịch...
Đọc tiếp
Quan sát đồ thị hàm số \(y = \sin x\) ở Hình 25.
a) Nêu tập giá trị của hàm số \(y = \sin x\)
b) Gốc tọa độ có là tâm đối xứng của đồ thị hàm số không? Từ đó kết luận tính chẵn, lẻ của hàm số \(y = \sin x\)
c) Bằng cách dịch chuyển đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) song song với trục hoành sang phải theo đoạn có độ dài \(2\pi \), ta có nhận được đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ {\pi ;3\pi } \right]\) hay không? Hàm số \(y = \sin x\)có tuần hoàn hay không/
d) Tìm khoảng đồng biến, nghịch biến của hàm số \(y = \sin x\)
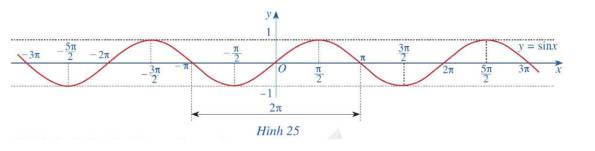
a) Tập giá trị của hàm số\(y = \sin x\) là \(\left[ { - 1;1} \right]\)
b) Đồ thị hàm số \(y = \sin x\) nhận O là tâm đối xứng.
Như vậy hàm số \(y = \sin x\) là hàm số lẻ.
c) Bằng cách dịch chuyển đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) song song với trục hoành sang phải theo đoạn có độ dài \(2\pi \), ta nhận được đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ {\pi ;3\pi } \right]\)
Như vậy, hàm số \(y = \sin x\) có tuần hoàn .
d) Hàm số \(y = \sin x\) đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\), nghịch biến trên mỗi khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right)\) với \(k \in Z\)
Đúng 0
Bình luận (0)
Quan sát đồ thị hàm số y cot x ở Hình 32.a) Nêu tập giá trị của hàm số y cot xb) Gốc tọa độ có là tâm đối xứng của đồ thị hàm số không? Từ đó kết luận tính chẵn, lẻ của hàm số y cot xc) Bằng cách dịch chuyển đồ thị hàm số y cot x trên khoảng left( {0;pi } right) song song với trục hoành sang phải theo đoạn có độ dài pi , ta nhận được y cot x trên khoảng left( {pi ;2pi } right) hay không? Hàm số y cot x có tuần hoàn hay không?d) Tìm khoảng đồng biến, nghịch biến của hàm số y...
Đọc tiếp
Quan sát đồ thị hàm số \(y = \cot x\) ở Hình 32.
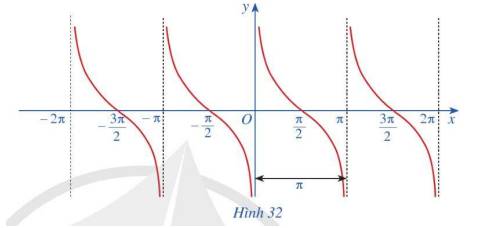
a) Nêu tập giá trị của hàm số \(y = \cot x\)
b) Gốc tọa độ có là tâm đối xứng của đồ thị hàm số không? Từ đó kết luận tính chẵn, lẻ của hàm số \(y = \cot x\)
c) Bằng cách dịch chuyển đồ thị hàm số \(y = \cot x\) trên khoảng \(\left( {0;\pi } \right)\) song song với trục hoành sang phải theo đoạn có độ dài \(\pi \), ta nhận được \(y = \cot x\) trên khoảng \(\left( {\pi ;2\pi } \right)\) hay không? Hàm số \(y = \cot x\) có tuần hoàn hay không?
d) Tìm khoảng đồng biến, nghịch biến của hàm số \(y = \cot x\)
a) Tập giá trị của hàm số \(y = \cot x\)là R
b) Gốc tọa độ là tâm đối xứng của đồ thị hàm số
Hàm số \(y = \cot x\)là hàm số lẻ
c) Bằng cách dịch chuyển đồ thị hàm số \(y = \cot x\) trên khoảng \(\left( {0;\pi } \right)\) song song với trục hoành sang phải theo đoạn có độ dài \(\pi \), ta nhận được \(y = \cot x\) trên khoảng \(\left( {\pi ;2\pi } \right)\)
Hàm số \(y = \cot x\) có tuần hoàn
d) Hàm số \(y = \cot x\)nghịch biến trên mỗi khoảng \(\left( {k\pi ;\pi + k\pi } \right),k \in Z\)
Đúng 0
Bình luận (0)
khẳng định nào sau đây là sai
a) Hàm số \(y=x^2+cosx\)là hàm số chẵn
b)hàm số\(y=|sinx-x|-|sinx+x|\)là hàm số lẻ
c) hàm số\(y=\frac{sinx}{x}\)là hàm số chẵn
d) hàm số y=sinx+2 là hàm số không chẵn không lẻ
1. Mệnh đề nào dưới đây sai ?A. Hàm số y tan x là hàm số lẻ. B. Hàm số y sin x là hàm số lẻC. Hàm số y Cot x là hàm số lẻ D. Hàm số y Cos x là hàm số lẻ2. Hàm số nào sau đây là hàm số lẻ?A. y Cos3x B. y Sinx + Cos3xC. y Sinx + Tan3x D. Tan2x3. Trong các hàm số sau, hàm số nào là hàm số chẵnA. y Cos2x B. y Cot2xC. y tan2x D. y sin2x4. Trong các hàm số sau, hàm số nào là hàm số lẻ?A. y Sinx Co...
Đọc tiếp
1. Mệnh đề nào dưới đây sai ?
A. Hàm số y = tan x là hàm số lẻ. B. Hàm số y = sin x là hàm số lẻ
C. Hàm số y = Cot x là hàm số lẻ D. Hàm số y = Cos x là hàm số lẻ
2. Hàm số nào sau đây là hàm số lẻ?
A. y = Cos3x B. y = Sinx + Cos3x
C. y = Sinx + Tan3x D. Tan2x
3. Trong các hàm số sau, hàm số nào là hàm số chẵn
A. y = Cos2x B. y = Cot2x
C. y = tan2x D. y = sin2x
4. Trong các hàm số sau, hàm số nào là hàm số lẻ?
A. y = Sinx Cos3x
B. y = Cosx + Sin2x
C. y = Cosx + Sinx
D. y = - Cosx
5. Hàm số nào là hàm số chẵn ?
A. y = Cosx
B. y = Sin x/2
C. y = tan2x
D. y = Cotx
Trong các hàm số sau, hàm số nào là hàm số chẵn, hàm số nào là hàm số lẻ:
\(y=5x^6;y=24x;y=-11x;y=\frac{2}{3}x^4;y=\sqrt{3}x^3;y=x^{10}\)
a) Biết rằng với x = 4 thì hàm số y = 3x + b có giá trị là 11. Tìm b. Vẽ đồ thị của hàm số với giá trị B vừa tìm được.
b) Biết rằng đồ thị của hàm số y = ax + 5 đi qua điểm A(-1; 3). Tìm a. Vẽ đồ thị hàm số với giá trị a tìm được
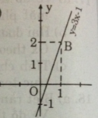
a) Thay x = 4 và y = 11 vào y = 3x + b ta được:
11 = 3.4 + b = 12 + b
=> b = 11 – 12 = -1
Ta được hàm số y = 3x – 1
- Cho x = 0 => y = -1 được A(0; -1)
- Cho x = 1 => y = 2 được B(1; 2).
Nối A, B ta được đồ thị hàm số y = 3x – 1.
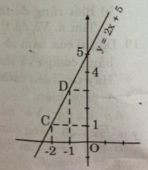
b) Thay tọa độ điểm A(-1; 3) vào phương trình y = ax + 5 ta có:
3 = a(-1) + 5
=> a = 5 – 3 = 2
Ta được hàm số y = 2x + 5.
- Cho x = -2 => y = 1 được C(-2; 1)
- Cho x = -1 => y = 3 được D(-1; 3)
Nối C, D ta được đồ thị hàm số y = 2x + 5.
Đúng 0
Bình luận (0)
Cho hai hàm số y f(x) và y g(x) xác định trên R. Đặt S(x) f(x) + g(x) và P(x) f(x) g(x).Xét các mệnh đề:i) Nếu y f(x) và y g(x) là những hàm số chẵn thì y S(x) và y P(x) cũng là những hàm số chẵnii) Nếu y f(x) và y g(x) là những hàm số lẻ thì y S(x) là hàm số lẻ và y P(x) là hàm số chẵniii) Nếu y f(x) là hàm số chẵn, y g(x) là hàm số lẻ thì y P(x) là hàm số lẻSố mệnh đề đúng là: A. 1 B. 2 C. 3 D. Tất cả đều sai
Đọc tiếp
Cho hai hàm số y = f(x) và y = g(x) xác định trên R. Đặt S(x) = f(x) + g(x) và P(x) = f(x) g(x).
Xét các mệnh đề:
i) Nếu y = f(x) và y = g(x) là những hàm số chẵn thì y = S(x) và y = P(x) cũng là những hàm số chẵn
ii) Nếu y = f(x) và y = g(x) là những hàm số lẻ thì y = S(x) là hàm số lẻ và y = P(x) là hàm số chẵn
iii) Nếu y = f(x) là hàm số chẵn, y = g(x) là hàm số lẻ thì y = P(x) là hàm số lẻ
Số mệnh đề đúng là:
A. 1
B. 2
C. 3
D. Tất cả đều sai
Biết rằng với x = 4 thì hàm số y = 3x + b có giá trị là 11.
a) Tìm b. Vẽ đồ thị của hàm số với giá trị của b vừa tìm được.
b) Biết rằng đồ thị của hàm số của hàm số y = ax + 5 đi qua điểm A(–1 ; 3). Tìm a. Vẽ đồ
thị của hàm số với giá trị của a vừa tìm được.