Cho tam giác ABC, M và N là hai điểm thỏa mãn: BM → = BC → - 2 AB → ; C N → = x A C → - B C → . Xác định x để A, M, N thẳng hàng
A. 3
B. - 1 3
C. 2
D. - 1 2
Những câu hỏi liên quan
26 tháng 12 2020 lúc 12:16
Cho tam giác ABC và M là trung điểm BC.a) Chứng minh rằng: \(\overrightarrow{AM}+\overrightarrow{BC}=\overrightarrow{BM}+\overrightarrow{AC}\)b) Cho hai điểm E,K thỏa mãn: \(\overrightarrow{EA}=-3\overrightarrow{EM}\) và \(5\overrightarrow{AK}=3\overrightarrow{AC}\). Chứng minh ba điểm B,E,K thẳng hàng.
a.
\(\overrightarrow{AM}+\overrightarrow{BC}=\overrightarrow{AC}+\overrightarrow{CM}+\overrightarrow{BM}+\overrightarrow{MC}=\overrightarrow{AC}+\overrightarrow{BM}\)
b.
\(\overrightarrow{AE}=3\overrightarrow{EM}=3\overrightarrow{EA}+3\overrightarrow{AM}\Rightarrow4\overrightarrow{AE}=3\overrightarrow{AM}\Rightarrow\overrightarrow{AE}=\dfrac{3}{4}\overrightarrow{AM}\)
\(\Rightarrow\overrightarrow{AE}=\dfrac{3}{4}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)=\dfrac{3}{8}\overrightarrow{AB}+\dfrac{3}{8}\overrightarrow{AC}\)
\(\overrightarrow{BE}=\overrightarrow{BA}+\overrightarrow{AE}=-\overrightarrow{AB}+\dfrac{3}{8}\overrightarrow{AB}+\dfrac{3}{8}\overrightarrow{AC}=-\dfrac{5}{8}\overrightarrow{AB}+\dfrac{3}{8}\overrightarrow{AC}\)
\(\overrightarrow{BK}=\overrightarrow{BA}+\overrightarrow{AK}=-\overrightarrow{AB}+\dfrac{3}{5}\overrightarrow{AC}=\dfrac{8}{5}\overrightarrow{BE}\)
\(\Rightarrow\) B, E, K thẳng hàng
Đúng 2
Bình luận (0)
cho tam giác ABC có A=90, BC=2a.
a)Giả sử điểm A thay đổi sao cho BAC=90,BC=2a.Tam giác ABC phải thỏa mãn điều kiện gì để diện tích tam giác AHO lớn nhất
b)gọi O là trung điểm của BC, M là trung điểm của AC, AO cắt BM tại G. Giả sử CG cắt AB tại N. Tứ giác AMON là hình gì? Tam giác ABC phải thỏa mãn điều kiện gì để diện tích tứ giác AMON lớn nhất?
Cho tam giác ABC. Trên cạnh AB lấy điểm M và trên cạnh AC lấy N sao cho thỏa mãn BM+CN=BC. Tia phân giác góc ABC và tia phân giác góc ACB cắt nhau ở I.
a) C/m IM=IN
b) C/m AI là tia phân giác của góc BAC .
(Gợi ý câu b: trên cạnh BC lấy K sao cho BK= BM)
Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của AC, AB. P và Q lần lượt thuộc BM và CN sao cho BP = 1/3BM, CQ = 1/3CN
a) Tứ giác MNPQ là hình gì? vì sao?
b) Tam giác ABC phải thỏa mãn đ/k gì thì thì MNPQ là hình chữ nhật?
c) Tam giác ABC, BM, CN thỏa mãn đk gì thì MNPQ là hình thoi, hình vuông
Cho hình chữ nhật ABCD có AB 2, AD 4, điểm M thuộc cạnh BC thỏa mãn BM 1. Điểm N thuộc đường chéo AC thỏa mãn
A
N
→
x
A
C
→
. Giá trị của x để tam giác AMN vuông tại M là A. 5/8 B. 5/4 C. 5/16 D. 0, 5
Đọc tiếp
Cho hình chữ nhật ABCD có AB = 2, AD = 4, điểm M thuộc cạnh BC thỏa mãn BM = 1. Điểm N thuộc đường chéo AC thỏa mãn A N → = x A C → . Giá trị của x để tam giác AMN vuông tại M là
A. 5/8
B. 5/4
C. 5/16
D. 0, 5
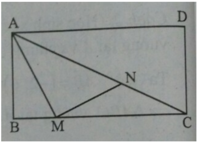
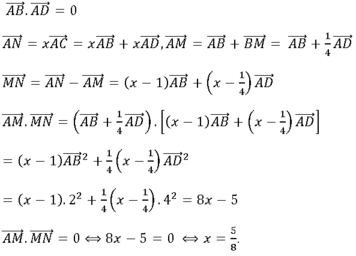
Chọn A.
Chú ý: Nếu có đúng bốn phương án như trong đề thi thì có thể dự đoán ngay phương án A sau khi vẽ hình
Đúng 0
Bình luận (0)
Cho tam giác ABC. Tập hợp các điểm M thỏa mãn
M
B
→
-
M
C
→
B
M
→
-...
Đọc tiếp
Cho tam giác ABC. Tập hợp các điểm M thỏa mãn M B → - M C → = B M → - B A → là?
A. đường thẳng AB
B. trung trực đoạn BC
C. đường tròn tâm A; bán kính BC
D. đường thẳng qua A và song song với BC
Cho tam giác ABC. Tập hợp các điểm M thỏa mãn
M
B
→
-
M
C
→
B
M
→
-
B...
Đọc tiếp
Cho tam giác ABC. Tập hợp các điểm M thỏa mãn M B → - M C → = B M → - B A → là?
A. đường thẳng AB
B. trung trực đoạn BC
C. đường tròn tâm A: bán kính BC
D. đường thẳng qua A và song song với BC
Ta có
Mà A; B; C cố định nên tập hợp điểm M là đường tròn tâm A, bán kính BC.
Chọn C
Đúng 0
Bình luận (0)
Tam giác ABC cố định trên tia đối của BC lấy M trên tia đối của tia CA lấy N sao cho BM=CN(1) Khi M và N di động thỏa mãn (1) thì trung điểm I của MN di động trên đường nào
Cho tam giác ABC và điểm M thuộc cạnh BC thỏa mãn tam giác AMB=tam giác AMC. Chứng minh rằng:
a)M là trung điểm của BC
b)Tia AM là phân giác của góc BAC và AM Vuông góc BC
a: ΔABM=ΔACM
=>BM=CM
=> M là trung điểm của BC
b: ΔAMC=ΔAMB
=>góc MAC=góc MAB và AC=AB
=>AM là phân giác của góc BAC
AB=AC
MB=MC
=>AM là trung trực của BC
=>AM vuông góc BC
Đúng 0
Bình luận (0)