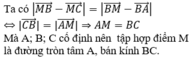Các câu hỏi tương tự
Câu 1: cho tam ABC. Có bao nhiêu điểm M thỏa mãn | vecto MA+vectoMB+vectoMC| 3a.1b.2c.3d. vô sốCâu 2: cho tam giác ABC đều cạnh a. biết rằng tập hợp các điểm M thỏa mãn đẳng thức |2vectoMA+3vectoMB+4vectoMC||vectoMB-vectoMA| là đường tròn cố định có bán kính R. tính bán kính R theo A?Câu 3: Cho 2 điểm A.B phân biệt và cố định, với I là trung điểm của AB. Tập hợp các điểm M thỏa mãn đẳng thức |2vectoMA+vectoMB||vectoMA+2vectoMB| là:a. đường trung trực của đoạn thẳng ABb. đường tròn đường kính AB...
Đọc tiếp
Câu 1: cho tam ABC. Có bao nhiêu điểm M thỏa mãn | vecto MA+vectoMB+vectoMC| = 3
a.1
b.2
c.3
d. vô số
Câu 2: cho tam giác ABC đều cạnh a. biết rằng tập hợp các điểm M thỏa mãn đẳng thức |2vectoMA+3vectoMB+4vectoMC|=|vectoMB-vectoMA| là đường tròn cố định có bán kính R. tính bán kính R theo A?
Câu 3: Cho 2 điểm A.B phân biệt và cố định, với I là trung điểm của AB. Tập hợp các điểm M thỏa mãn đẳng thức |2vectoMA+vectoMB|=|vectoMA+2vectoMB| là:
a. đường trung trực của đoạn thẳng AB
b. đường tròn đường kính AB
c. đường trung trực của đoạn thẳng IA
d. đường tròn tâm A, bán kính AB
Câu 1: Cho 2 điểm A,B phân biệt và cố định, với I là trung điểm của AB. Tập hợp các điểm M thỏa mãn đẳng thức left|2.vectoMA+vectoMBright|left|vectoMA+2.vectoMBright|là:A. đường trung trực của đoạn ABB. đường tròn đường kính ABC. đường trung trực đoạn thẳng IAD. đường tròn tâm A, bán kính ABCâu 2: cho tam giác ABC đều cạnh a. Biết rằng tập hợp các điểm M thỏa mãn đẳng thức left|3.vectoMA+3.vectoMB+4.vectoMCright|left|vectoMB-vectoMAright|là đường tròn cố định có bán kính R. Tính bán kính R theo...
Đọc tiếp
Câu 1: Cho 2 điểm A,B phân biệt và cố định, với I là trung điểm của AB. Tập hợp các điểm M thỏa mãn đẳng thức \(\left|2.vectoMA+vectoMB\right|=\left|vectoMA+2.vectoMB\right|\)là:
A. đường trung trực của đoạn AB
B. đường tròn đường kính AB
C. đường trung trực đoạn thẳng IA
D. đường tròn tâm A, bán kính AB
Câu 2: cho tam giác ABC đều cạnh a. Biết rằng tập hợp các điểm M thỏa mãn đẳng thức \(\left|3.vectoMA+3.vectoMB+4.vectoMC\right|=\left|vectoMB-vectoMA\right|\)là đường tròn cố định có bán kính R. Tính bán kính R theo a.
A. R = a/3
B. R = a/9
C. R = a/2
D. R = a/6
Câu 3: Cho hình chữ nhật ABCD và số thực K>0. Tập hợp các điểm M thỏa mãn đẳng thức \(\left|vectoMA+vectoMB+vectoMC+vectoMD\right|=k\)là:
A. một đoạn thẳng
B. một đường thẳng
C. một đường tròn
D. một điểm
Câu 4:Cho tam giác ABC. Có bao nhiêu điểm M thỏa mãn \(\left|vectoMA+vectoMB+vectoMC\right|=3\)?
A.1
B.2
C.3
D. vô số
Cho tam giác ABC nhọn với ABBC và D là điểm thuộc cạnh BC sao cho AD là phân giác của
B
A
C
^
. Đường thẳng qua C và song song với AD, cắt trung trực của AC tại E. Đường thẳng qua B song song với AD, cắt trung trực của AB tại F.1) Chứng minh rằng tam giác ABF đồng dạng với tam giác ACE.2). Chứng minh rằng các đường thẳng
B
E
;
C
F
;...
Đọc tiếp
Cho tam giác ABC nhọn với AB<BC và D là điểm thuộc cạnh BC sao cho AD là phân giác của B A C ^ .
Đường thẳng qua C và song song với AD, cắt trung trực của AC tại E.
Đường thẳng qua B song song với AD, cắt trung trực của AB tại F.
1) Chứng minh rằng tam giác ABF đồng dạng với tam giác ACE.
2). Chứng minh rằng các đường thẳng B E ; C F ; A D đồng quy tại một điểm, gọi điểm đó là G.
3). Đường thẳng qua G song song với AE cắt đường thẳng BF tại Q. Đường thẳng QE, cắt đường tròn ngoại tiếp tam giác GEC tại P khác E. Chứng minh rằng các điểm A, P, G, Q, F cùng thuộc một đường tròn.
Cho tam giác ABC nhọn không cân nội tiếp đường tròn (O). D là điểm thuộc cạnh BC (D khác B và D khác C).Trung trực của CA; AB lần lượt cắt đường thẳng AD tại E, F. Đường thẳng qua E song song với AC cắt tiếp tuyến qua C của (O) tại M. Đường thẳng qua F song song với AB cắt tiếp tuyến qua B của (O) tại N. 2) Giả sử
F
N
E
M
B
N...
Đọc tiếp
Cho tam giác ABC nhọn không cân nội tiếp đường tròn (O).
D là điểm thuộc cạnh BC (D khác B và D khác C).
Trung trực của CA; AB lần lượt cắt đường thẳng AD tại E, F.
Đường thẳng qua E song song với AC cắt tiếp tuyến qua C của (O) tại M.
Đường thẳng qua F song song với AB cắt tiếp tuyến qua B của (O) tại N.
2) Giả sử F N E M = B N C M . Chứng minh rằng AD là phân giác của tam giác ABC.
Cho tam giác ABC nhọn không cân nội tiếp đường tròn (O). D là điểm thuộc cạnh BC (D khác B và D khác C).Trung trực của CA; AB lần lượt cắt đường thẳng AD tại E, F. Đường thẳng qua E song song với AC cắt tiếp tuyến qua C của (O) tại M. Đường thẳng qua F song song với AB cắt tiếp tuyến qua B của (O) tại N. 1) Chứng minh rằng đường thẳng MN tiếp xúc với (O).
Đọc tiếp
Cho tam giác ABC nhọn không cân nội tiếp đường tròn (O). D là điểm thuộc cạnh BC (D khác B và D khác C).
Trung trực của CA; AB lần lượt cắt đường thẳng AD tại E, F.
Đường thẳng qua E song song với AC cắt tiếp tuyến qua C của (O) tại M.
Đường thẳng qua F song song với AB cắt tiếp tuyến qua B của (O) tại N.
1) Chứng minh rằng đường thẳng MN tiếp xúc với (O).
Bài 5: (3,0 điểm) Cho tam giác ABC cân tại A, A là góc nhọn. M là trung điểm BC. Gọi D là điểm nằm giữa A và M.a) Cho AC 10cm, AM 8cm. Tính độ dài cạnh BCb) Vẽ đường thẳng d đi qua D và song song với BC, Vẽ đường thẳng đi qua B song song với AC và cắt d tại E, vẽ đường thẳng đi qua C song song với AB và cắt d tại F. Chứng minh tam giác AEF là tam giác
Đọc tiếp
Bài 5: (3,0 điểm) Cho tam giác ABC cân tại A, A là góc nhọn. M là trung điểm BC. Gọi D là điểm nằm giữa A và M.
a) Cho AC = 10cm, AM = 8cm. Tính độ dài cạnh BC
b) Vẽ đường thẳng d đi qua D và song song với BC, Vẽ đường thẳng đi qua B song song với AC và cắt d tại E, vẽ đường thẳng đi qua C song song với AB và cắt d tại F. Chứng minh tam giác AEF là tam giác
Cho tam giác nhọn ABC nội tiếp đường tròn tâm O. Gọi M là một điểm trên cung nhỏ
B
C
⏜
(M khác B; C và AM không đi qua O). Giả sử P là một điểm thuộc đoạn thẳng AM sao cho đường tròn đường kính MP cắt cung nhỏ BC tại điểm N khác M.1). Gọi D là điểm đối xứng với điểm M qua O. Chứng minh rằng ba điểm N, P, D thẳng hàng.2). Đường tròn đường kính MP cắt MD tại điểm Q khác M. Chứng minh rằng P là tâm đường tròn nội tiếp tam giác AQN.
Đọc tiếp
Cho tam giác nhọn ABC nội tiếp đường tròn tâm O.
Gọi M là một điểm trên cung nhỏ B C ⏜ (M khác B; C và AM không đi qua O).
Giả sử P là một điểm thuộc đoạn thẳng AM sao cho đường tròn đường kính MP cắt cung nhỏ BC tại điểm N khác M.
1). Gọi D là điểm đối xứng với điểm M qua O. Chứng minh rằng ba điểm N, P, D thẳng hàng.
2). Đường tròn đường kính MP cắt MD tại điểm Q khác M. Chứng minh rằng P là tâm đường tròn nội tiếp tam giác AQN.
Bài 1. Viết phương trình tổng quát, phương trình tham số của đường thẳng trong mỗi trường hợp sau:a) Đi qua A(1;-2) và // với đường thẳng 2x - 3y - 3 0.b) Đi qua hai điểm M(1;-1) và N(3;2).c) Đi qua điểm P(2;1) và vuông góc với đường thẳng x - y + 5 0.Bài 2. Cho tam giác ABC biết A(-4;1), B(2;4), C(2;-2).Tính khoảng cách từ điểm C đến đường thẳng AB.Bài 3. Cho tam giaùc ABC coù: A(3;-5), B(1;-3), C(2;-2).Vieát phöông trình toång quaùt cuûa:a) 3 caïnh AB, AC, BCb) Ñöôøng thaúng qua A vaø song...
Đọc tiếp
Bài 1. Viết phương trình tổng quát, phương trình tham số của đường thẳng trong mỗi trường hợp sau:
a) Đi qua A(1;-2) và // với đường thẳng 2x - 3y - 3 = 0.
b) Đi qua hai điểm M(1;-1) và N(3;2).
c) Đi qua điểm P(2;1) và vuông góc với đường thẳng x - y + 5 = 0.
Bài 2. Cho tam giác ABC biết A(-4;1), B(2;4), C(2;-2).
Tính khoảng cách từ điểm C đến đường thẳng AB.
Bài 3. Cho tam giaùc ABC coù: A(3;-5), B(1;-3), C(2;-2).Vieát phöông trình toång quaùt cuûa:
a) 3 caïnh AB, AC, BC
b) Ñöôøng thaúng qua A vaø song song vôùi BC
c)Trung tuyeán AM vaø ñöôøng cao AH cuûa tam giaùc ABC
d) Ñöôøng thaúng qua troïng taâm G cuûa tam giaùc ABC vaø vuoâng goùc vôùi AC
e) Ñöôøng trung tröïc cuûa caïnh BC
Bài 4. Cho tam giaùc ABC coù: A(1 ; 3), B(5 ; 6), C(7 ; 0).:
a) Vieát phöông trình toång quaùt cuûa 3 caïnh AB, AC, BC
b) Viết phương trình đđöôøng trung bình song song cạnh AB
c) Viết phương trình đường thẳng qua A và cắt hai trục tọa độ tại M,N sao cho AM = AN
d) Tìm tọa độ điểm A’ là chân đường cao kẻ từ A trong tam giaùc ABC
Bài 5. Viết phương trình đường tròn có tâm I(1; -2) và
a) đi qua điểm A(3;5).
b) tiếp xúc với đường thẳng có pt x + y = 1.
Bài 10:Cho ABC có a 8, b 10, c 13 a. ABC có góc tù hay không ? Tính bán kính đường tròn ngoại tiếp ABC. b. Tính diện tích ABC Bài 11:Cho tam giác ABC có: a 6, b 7, c 5. a) Tính S ,h ,R,r ABC a b) Tính bán kính đường tròn đi qua A, C và trung điểm M của cạnh AB.Bài 12:Cho tam giác ABC có: AB 6, BC 7, AC 8. M trên cạnh AB sao cho MA 2 MB. a) Tính các góc của tam giác ABC. b) Tính S ,h ,R ABC a , r. c) Tính bán kính đường tròn ngoại tiếp ∆MBC.Bài 13:Cho ABC có 0 0 A B b 60 , 45 , 2...
Đọc tiếp
Bài 10:Cho ABC có a = 8, b =10, c =13 a. ABC có góc tù hay không ? Tính bán kính đường tròn ngoại tiếp ABC. b. Tính diện tích ABC
Bài 11:Cho tam giác ABC có: a = 6, b = 7, c = 5. a) Tính S ,h ,R,r ABC a b) Tính bán kính đường tròn đi qua A, C và trung điểm M của cạnh AB.
Bài 12:Cho tam giác ABC có: AB = 6, BC = 7, AC = 8. M trên cạnh AB sao cho MA = 2 MB. a) Tính các góc của tam giác ABC. b) Tính S ,h ,R ABC a , r. c) Tính bán kính đường tròn ngoại tiếp ∆MBC.
Bài 13:Cho ABC có 0 0 A B b = = = 60 , 45 , 2 tính độ dài cạnh a, c, bán kính đường tròn ngoại tiếp và diện tích tam giác ABC
Bài 14:Cho ABC AC = 7, AB = 5 và 3 cos 5 A = . Tính BC, S, a h , R, r.
Bài 15:Cho ABC có 4, 2 m m b c = = và a =3 tính độ dài cạnh AB, AC.
Bài 16:Cho ABC có AB = 3, AC = 4 và diện tích S = 3 3 . Tính cạnh BC
Bài 17:Cho tam giác ABC có ˆ o A 60 = , c h 2 3 = , R = 6. a) Tính độ dài các cạnh của ∆ABC. b) Họi H là trực tâm tam giác ABC. Tính bán kính đường tròn ngoại tiếp ∆AHC.
Bài 18:a. Cho ABC biết 0 0 a B C = = = 40,6; 36 20', 73 . Tính BAC , cạnh b,c. b.Cho ABC biết a m = 42,4 ; b m = 36,6 ; 0 C = 33 10' . Tính AB, và cạnh c.
Bài 19:Tính bán kính đường tròn nội tiếp ABC biết AB = 2, AC = 3, BC = 4.
Bài 20:Cho ABC biết A B C (4 3; 1 , 0;3 , 8 3;3 − ) ( ) ( ) a. Tính các cạnh và các góc của ABC b. Tính chu vi và diện tích ABC
Cho tam giác nhọn ABC nội tiếp đường tròn tâm O.Gọi M là một điểm trên cung nhỏ
B
C
⏜
(M khác B; C và AM không đi qua O).Giả sử P là một điểm thuộc đoạn thẳng AM sao cho đường tròn đường kính MP cắt cung nhỏ BC tại điểm N khác M.2). Đường tròn đường kính MP cắt MD tại điểm Q khác M. Chứng minh rằng P là tâm đường tròn nội tiếp tam giác AQN.
Đọc tiếp
Cho tam giác nhọn ABC nội tiếp đường tròn tâm O.
Gọi M là một điểm trên cung nhỏ B C ⏜ (M khác B; C và AM không đi qua O).
Giả sử P là một điểm thuộc đoạn thẳng AM sao cho đường tròn đường kính MP cắt cung nhỏ BC tại điểm N khác M.
2). Đường tròn đường kính MP cắt MD tại điểm Q khác M. Chứng minh rằng P là tâm đường tròn nội tiếp tam giác AQN.