Cho hình hộp ABCD.A’B’C’D’. Mặt phẳng (AB’D’) song song với mặt phẳng nào sau đây?
A. (BA’C’).
B. (C’BD).
C. (BDA’).
D. (ACD’).
Cho hình hộp ABCD.A’B’C’D’. Mặt phẳng (AB’D’) song song với mặt phẳng
A. (ABCD)
B. (BCC’B’)
C. (BDA’)
D. (BDC’)
Cho hình hộp A B C D . A ' B ' C ' D ' , và một điểm M nằm giữa hai điểm A và B. Gọi (P) là mặt phẳng đi qua M và song song với mặt phẳng (AB’D’). Cắt hình hộp bởi mặt phẳng (P) thì thiết diện là :
A. Hình ngũ giác
B. Hình lục giác
C. Hình tam giác
D. Hình tứ giác
Cho hình hộp ABCD.A’B’C’D’.
a) Chứng minh rằng hai mặt phẳng (BDA’) và (B’D’C) song song với nhau.
b) Chứng minh rằng đường chéo AC’ đi qua trọng tâm G1 và G2 lần lượt của hai tam giác BDA’ và B’D’C.
c) Chứng minh G1 và G2 chia đoạn AC’ thành ba phần bằng nhau.
d) Gọi O và I lần lượt là tâm các hình bình hành ABCD và AA’C’C. Xác định thiết diện của mặt phẳng (A’IO) với hình hộp đã cho.
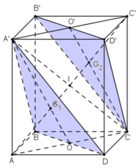
a) + A’D’ // BC và A’D’ = BC
⇒ A’D’CB là hình bình hành
⇒ A’B // D’C, mà D’C ⊂ (B’D’C) ⇒ A’B // (B’D’C) (1)
+ BB’ // DD’ và BB’ = DD’
⇒ BDD’B’ là hình bình hành
⇒ BD // B’D’, mà B’D’ ⊂ (B’D’C) ⇒ BD // (B’D’C) (2)
A’B ⊂ (BDA’) và BD ⊂ (BDA’); A’B ∩ BD = B (3)
Từ (1), (2), (3) suy ra : (BDA’) // (B’D’C).
b) Gọi O = AC ∩ BD
+ Ta có: O ∈ AC ⊂ (AA’C’C)
⇒ A’O ⊂ (AA’C’C).
Trong (AA’C’C), gọi A’O ∩ AC’ = G1.
G1 ∈ A’O ⊂ (A’BD)
⇒ G1 ∈ AC’ ∩ (BDA’).
+ Trong hình bình hành AA’C’C gọi I = A’C ∩ AC’
⇒ A’I = IC.
⇒ AI là trung tuyến của ΔA’AC
⇒ G 1 = A ’ O ∩ A C ’ là giao của hai trung tuyến AI và A’O của ΔA’AC
⇒ G 1 là trọng tâm ΔA’AC
⇒ A ’ G 1 = 2 . A ’ O / 3
⇒ G 1 cũng là trọng tâm ΔA’BD.
Vậy AC' đi qua trọng tâm G 1 của ΔA’BD.
Chứng minh tương tự đối với điểm G 2 .
c) *Vì G 1 là trọng tâm của ΔAA’C nên A G 1 / A I = 2 / 3 .
Vì I là trung điểm của AC’ nên AI = 1/2.AC’
Từ các kết quả này, ta có : A G 1 = 1 / 3 . A C ’
*Chứng minh tương tự ta có : C ’ G 2 = 1 / 3 . A C ’
Suy ra : A G 1 = G 1 G 2 = G 2 C ’ = 1 / 3 . A C ’ .
d) (A’IO) chính là mp (AA’C’C) nên thiết diện cần tìm chính là hình bình hành AA’C’C.
Cho hình hộp ABCD.A’B’C’D’. Hai điểm M và N lần lượt nằm trên hai cạnh AD và CC’ sao cho: A M M D = C N N C '
a) Chứng minh rằng đường thẳng MN song song với mặt phẳng (ACB’)
b) Xác định thiết diện của hình hộp cắt bởi mặt phẳng đi qua MN và song song với mặt phẳng (ACB’)
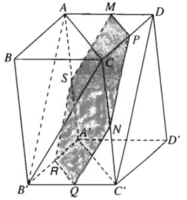
a) Vẽ MP song song với AC và cắt CD tại P
Ta có: 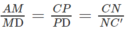
Do đó PN // DC′ // AB′
Đường thẳng MN thuộc mặt phẳng (MNP) và mặt phẳng này có MP // AC và PN // AB′. Vậy mặt phẳng(MNP) song song với mặt phẳng (ACB’) và do đó MN // (ACB′)
b) Vì mặt phẳng (MNP) song song với mặt phẳng (ACB’) nên hai mặt phẳng đó cắt các mặt bên của hình hộp theo các giao tuyến song song.
Ta vẽ NQ // CB′, QR // C′A′ ((// CA), RS //AB′ (//PN) và tất nhiên SM // QN. Thiết diện của hình hộp cắt bởi mặt phẳng đi qua MN và song song với mặt phẳng (ACB’) là hình lục giác MPNQRS có các cạnh đối diện song song với nhau từng đôi một: MP // RQ, PN //SR, NQ // MS.
Cho hình hộp ABCD.A’B’C’D’ có tất cả các mặt là hình vuông cạnh a. Các điểm M,N lần lượt nằm trên AD’, DB sao cho AM=DN=x, ( 0 < x < a 2 ). Khi x thay đổi, đường thẳng MN luôn song song với mặt phẳng cố định nào sau đây
A. (CB’D’)
B. (A’BC)
C. (AD’C)
D. (BA’C’)
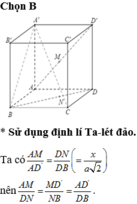
Áp dụng định lí Ta-lét đảo, ta có AD, MN, BD’ lần lượt nằm trên ba mặt phẳng song song.
=> M song song với mặt phẳng (P) chứa BD’ và song song với AD.
Nên MN//(BCD’A’) hayMN//(A’BC).
Cho hình lăng trụ ABCD.A’B’C’D”. Gọi H là trung điểm của A’B’. Đường thẳng B’C song song với mặt phẳng nào sau đây?
A. ( AHC’)
B. (AA’H)
C. ( HAB)
D. ( HA’C’)
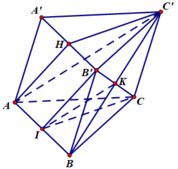
Gọi K là giao điểm của B’C và BC’, I là trung điểm của AB.
Do HB’= AI và HB’ //AI nên AHB’I là hình bình hành
=> AH// B’I.
Mặt khác : KI// AC’ nên (AHC’) // (B’CI).
Do đó: B’C //(AHC’).
Chọn A.
1.Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi A',B' lần lượt là trung điểm của SA,SB . Đường thẳng A' B' song song với mặt phẳng nào dưới đây?
A. (SAB).
B. ( ABCD) .
C. (SAD).
D. (SBC).
2.Cho hình hộp ABCD.A' B' C' D' . Mặt phẳng ( ABA') song song với:
A. ( AA'C') .
B. (CC'D').
C. ( ADD').
D. (BB'A').
Cho hình hộp ABCD.A’B’C’D. Chứng minh rằng hai mặt phẳng (ADD’A’) và (BCC’B’) song song với nhau.
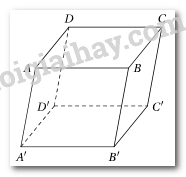
Ta có: ABCD là hình bình hành suy ra AD // BC suy ra AD // (BCC'B').
ABCD.A'B'C'D' là hình hộp suy ra DD'//CC' suy ra DD' // (BCC'B').
(ADD'A') chứa cặp cạnh cắt nhau song song với (BCC'B') nên (ADD'A') //(BCC'B').
Cho hình hộp A'B'C'D'.ABCD, xác định tiết diện của hình hộp tạo bởi mặt phẳng P đi qua điểm M bất kì nằm trên cạnh BC và mặt phẳng P song song với mặt phẳng ACD'