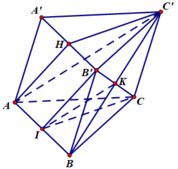
Gọi K là giao điểm của B’C và BC’, I là trung điểm của AB.
Do HB’= AI và HB’ //AI nên AHB’I là hình bình hành
=> AH// B’I.
Mặt khác : KI// AC’ nên (AHC’) // (B’CI).
Do đó: B’C //(AHC’).
Chọn A.
Cho hình lăng trụ ABC.A'B'C'. Gọi H là trung điểm của A'B'. Đường thẳng B'C song song với mặt phẳng nào sau đây?
A. (AHC')
B. (AA'H)
C. (HAB)
D. (HA'C')
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M và M’ lần lượt là trung điểm của các cạnh BC và B’C’.
a) Chứng minh rằng AM song song với A’M’.
b) Tìm giao điểm của mặt phẳng (A’B’C’) với đường thẳng A’M.
c) Tìm giao tuyến d của hai mặt phẳng (AB’C’) và (BA’C’).
d) Tìm giao điểm G của đường thẳng d với mp(AMA’). Chứng minh G là trọng tâm của tam giác AB’C’.
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi H là trung điểm của cạnh A’B’. Gọi d là giao tuyến của hai mặt phẳng (A’B’C’) và (A’BC). Thiết diện của hình lăng trụ khi cắt bởi mp(H,d) là hình gì?
A. Không xác định
B. Tam giác
C. Hình vuông
D. Hình bình hành
Cho hình hộp ABCD.A’B’C’D’ có AB =a, BB'= a 5 các đường thẳng A’B và B’C cùng tạo với mặt phẳng (ABCD) một góc 45 0 tam giác A’AB vuông tại B, tam giác A’CD vuông tại D. Tính thể tích của khối hộp ABCD.A’B’C’D’ theo a
A. 2 a 3
B. 2 a 3 3
C. a 3 6 2
D. a 3 6 6
Cho hình lăng trụ ABC.A’B’C’. gọi I, J, K lần lượt là trọng tâm của các tam giác ABC, ACC’, A’B’C’. mặt phẳng nào sau đây song song với (IJK)?
A. (ABC)
B. (A’BC’)
C. (BB’C’)
D. (AA’C)
Cho hình hộp ABCD.A’B’C’D’. Gọi M, N lần lượt là trung điểm của CD và DD’; G và G’ lần lượt là trọng tâm của hai tứ diện A’D’NM và BCC’D’. Đặt A B → = a → ; A A ' → = b → ; A D → = c → .
Đường thẳng GG’ song song với mặt phẳng (AA’B’B) vì:
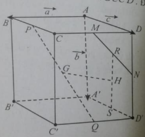
A. Vecto G G ' → cùng phương với vecto C D →
B. Vecto G G ' → cùng phương với vecto M N →
C. Vecto G G ' → đồng phẳng với hai vecto a → v à b →
D. Vecto G G ' → đồng phẳng với hai vecto b → v à c → .
Cho hình lăng trụ đứng ABC.A’B’C’có đáy là tam giác vuông và AB=BC=a, AA'= a 2 . Gọi M là trung điểm của BC. Tính khoảng cách d của hai đường thẳng AM và B’C
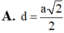
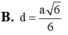
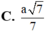
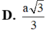
Cho hình hộp ABCD.A’B’C’D’. Hai điểm M và N lần lượt nằm trên hai cạnh AD và CC’ sao cho: A M M D = C N N C '
a) Chứng minh rằng đường thẳng MN song song với mặt phẳng (ACB’)
b) Xác định thiết diện của hình hộp cắt bởi mặt phẳng đi qua MN và song song với mặt phẳng (ACB’)
Cho khối lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình vuông. Hình chiếu vuông góc của A trên mặt phẳng (ABCD) là trung điểm của AB, góc giữa mặt phẳng (A’CD) và mặt phẳng (ABCD) là 60 0 . Thể tích khối chóp B’.ABCD là 8 3 a 3 2 Tính độ dài đoạn thẳng AC theo a
A. 2 a 3 3
B. 2 3 a 3 3
C. 2a
D. 2 2 a
