Cho hình hộp chữ nhật ABCD A'B'C'D' có A A ' = a , A B = a , A D = c . Tính bán kính đường tròn là giao tuyến của mặt phẳng A B C D với mặt cầu đi qua 8 đỉnh của hình hộp.
A. 1 2 a 2 + b 2 + c 2
B. 1 2 a 2 + b 2
C. 1 2 b 2 + c 2
D. 1 2 c 2 + a 2
Những câu hỏi liên quan
Cho hình hộp chữ nhật ABCD. A'B'C'D' có các kích thước là a, b, c (a < b < c). Hình hộp chữ nhật này có mấy mặt đối xứng
A. 1
B. 2
C. 3
D. 4
Chọn C.
Hình hộp chữ nhật ABCD. A’B’C’D’ có 3 mặt đối xứng, đó là các mặt phẳng trung trực AB, AD, AA’.
Đúng 0
Bình luận (0)
Cho hình hộp chữ nhật ABCD A'B'C'D'
a chứng minh rằng ABC'D' là hình chữ nhật
b tính thể tích hình hộp chữ nhật ABCD. A'B'C'D' biết ABCD là hình vuông có cạnh 3 cm và diện tích ABC'D' bằng 18 cm2
SGK Kết nối tri thức và cuộc sống
16 tháng 8 2023 lúc 18:10
Cho hình hộp chữ nhật ABCD. A'B'C'D'.
a) Chứng minh rằng (BDD′B′) \( \bot \) (ABCD).
b) Xác định hình chiếu của AC′ trên mặt phẳng (ABCD).
c) Cho AB = a, BC = b, CC′ = c. Tính AC′.
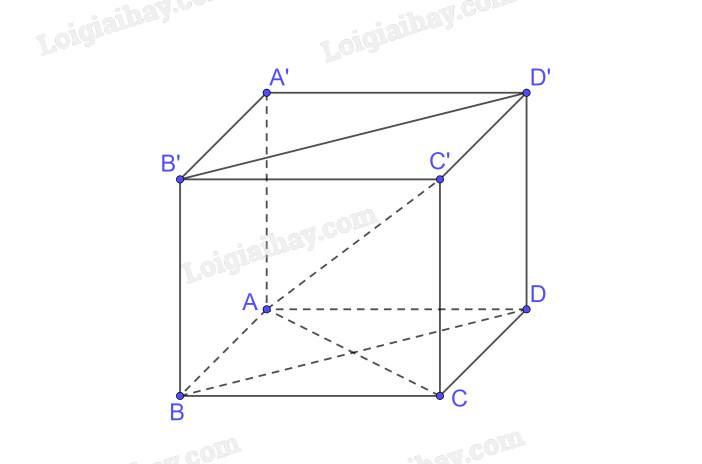
a) Ta có \(BB' \bot \left( {ABCD} \right);BB' \subset \left( {BDD'B'} \right) \Rightarrow \left( {BDD'B'} \right) \bot \left( {ABCD} \right)\)
b) A là hình chiếu của A trên (ABCD)
C là hình chiếu của C’ trên (ABCD) do \(CC' \bot \left( {ABCD} \right)\)
\( \Rightarrow \) AC là hình chiếu của AC’ trên (ABCD)
c) Xét tam giác ABC vuông tại B có
\(A{C^2} = A{B^2} + B{C^2} = {a^2} + {b^2} \Rightarrow AC = \sqrt {{a^2} + {b^2}} \)
Xét tam giác AC’C vuông tại C có
\(A{C'^2} = C{C'^2} + A{C^2} = {c^2} + {a^2} + {b^2} \Rightarrow A'C = \sqrt {{a^2} + {b^2} + {c^2}} \)
Đúng 0
Bình luận (0)
Cho hình hộp chữ nhật đứng
A
B
C
D
.
A
B
C
D
có
A
B
a
,
A
D...
Đọc tiếp
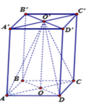
Cho hình hộp chữ nhật đứng A B C D . A ' B ' C ' D ' có A B = a , A D = a , A A ' = 3 a Gọi O ' là tâm hình chữ nhật A ' B ' C ' D ' Thể tích của khối chóp O ' . A B C D là?
A. 4 a 3
B. 2 a 3
C. a 3
D. 6 a 3
Đáp án B
Gọi O là tâm của hình chữ nhật ABCD thì O O ' = 3 a
V O ' A B C D = 1 3 O O ' . A B . A D = 2 a 3
Đúng 0
Bình luận (0)
Cho hình hộp chữ nhật ABCD. A'B'C'D'. Chứng minh :
a)(ABCD)song song với (A'B'C'D')
b)(ABB'A')song song với (CDD'C')
c)(BDC')song song với (AB'D')
Cho hình hộp chữ nhật ABCD. ABCD có đáy ABCD là hình vuông cạnh a, AAb. Gọi M là trung điểm của cạnh CC. Tính theo a và b thể tích V của khối tứ diện BDAM
Đọc tiếp
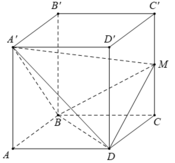
Cho hình hộp chữ nhật ABCD. A'B'C'D' có đáy ABCD là hình vuông cạnh a, AA'=b. Gọi M là trung điểm của cạnh CC'. Tính theo a và b thể tích V của khối tứ diện BDA'M
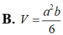
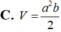
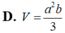
cho hình hộp chữ nhật ABCD. A'B'C'D' có AB= 10cm, BC=20cm,AA'=15cm
a) Tính thể tích hình hộp chữ nhật
b) Tính độ dài đường chéo AC' của hình hộp chữ nhật ( làm tròn đến chữ số thập phân thứ nhất ).
Cho hình hộp chữ nhật
A
B
C
D
.
A
B
C
D
có
A
B
a
,
A
D
a
2
,
A
B
a
5
.
Tính theo thể tích khối hợp đã cho. A.
V
2
a
3...
Đọc tiếp
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có A B = a , A D = a 2 , A B ' = a 5 . Tính theo thể tích khối hợp đã cho.
A. V = 2 a 3 2
B. V = a 3 10
C. V = a 3 2
D. V = 2 a 3 2 3
Đáp án A
Tam giác ABB’ vuông tại B ⇒ B B ' = A B ' 2 − A B 2 = 2 a ⇒ A A ' = 2 a .
Thể tích khối hộp A B C D . A ' B ' C ' D ' là V = 2 2 a 3
Đúng 0
Bình luận (0)
Cho hình hộp chữ nhật đứng ABCD.ABCD có ABa, AD2a, AA3a. Gọi O là tâm hình chữ nhật ABCD. Thể tích của khối chóp O.ABCD là? A.
4
a
3
B.
2
a
3
C.
a
3
D.
6
a
3
Đọc tiếp
Cho hình hộp chữ nhật đứng ABCD.A'B'C'D' có AB=a, AD=2a, AA'=3a. Gọi O' là tâm hình chữ nhật A'B'C'D'. Thể tích của khối chóp O'.ABCD là?
A. 4 a 3
B. 2 a 3
C. a 3
D. 6 a 3
